
Proprietăți de heptadecagon, diagonale, perimetru, suprafață

heptadecagon este un poligon regulat cu 17 laturi și 17 vârfuri. Construcția sa se poate face în stilul euclidian, adică folosind doar rigla și busola. A fost marele geniu matematic Carl Friedrich Gauss (1777-1855), de doar 18 ani, cel care a găsit procedura de construcție a acestuia în 1796.
Aparent, Gauss a fost întotdeauna foarte înclinat spre această figură geometrică, într-o asemenea măsură încât, din ziua în care a descoperit construcția sa, a decis să fie matematician. Se mai spune că a vrut ca heptadecagonul să fie gravat pe piatra sa funerară.

Gauss a găsit, de asemenea, formula pentru a determina care poligoane regulate au posibilitatea de a fi construite cu rigla și busola, deoarece unii nu au o construcție euclidiană exactă.
Indice articol
- 1 Caracteristicile heptadecagonului
- 2 Diagonale și perimetru
- 2.1 Perimetrul heptadecagonului
- 3 Zona
- 3.1 Suprafață dată lateral
- 3.2 Zona dată de raza
- 4 Exemple
- 4.1 Exemplul 1
- 4.2 Exemplul 2
- 5 Referințe
Caracteristicile heptadecagonului
În ceea ce privește caracteristicile sale, ca orice poligon, suma unghiurilor sale interne este importantă. Într-un poligon regulat de n laturi, suma este dată de:
Sa (n) = (n -2) * 180º.
Pentru heptadecagon numărul de laturi n este 17, ceea ce înseamnă că suma unghiurilor sale interne este:
Sa (17) = (17 - 2) * 180º = 15 * 180º = 2700º.
Această sumă, exprimată în radiani, arată astfel:
Sa (17) = (17 - 2) * π = 15 * π = 15π
Din formulele de mai sus se poate deduce cu ușurință că fiecare unghi intern al unui heptadecagon are o măsură exactă α dată de:
α = 2700º / 17 = (15/17) π radiani
Rezultă că unghiul intern în formă aproximativă este:
α ≈ 158,824º
Diagonale și perimetru
Diagonalele și perimetrul sunt alte aspecte importante. În orice poligon, numărul de diagonale este:
D = n (n - 3) / 2 iar în cazul heptadecagonului, ca n = 17, atunci este asta D = 119 diagonale.
Pe de altă parte, dacă se cunoaște lungimea fiecărei părți a heptadecagonului, atunci perimetrul heptadecagonului obișnuit se găsește pur și simplu adăugând de 17 ori acea lungime, sau ceea ce este echivalent cu 17 ori lungimea d De fiecare parte:
P = 17 zile
Perimetrul heptadecagonului
Uneori este cunoscută doar raza r a heptadecagonului, deci este necesar să se dezvolte o formulă pentru acest caz.
În acest scop, conceptul de apotemă. Apotema este segmentul care merge de la centrul poligonului regulat la punctul de mijloc al unei părți. Apotema relativă la o parte este perpendiculară pe acea parte (vezi figura 2).
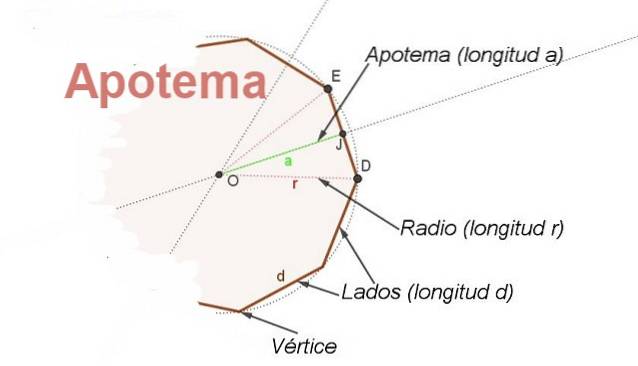
În plus, apotema este bisectoarea unghiului cu vârf central și laturi pe două vârfuri consecutive ale poligonului, acest lucru permite găsirea unei relații între raza r și lateral d.
Dacă se numește β spre unghiul central CĂPRIOARĂ și ținând cont că apotema JO este bisectoare aveți EJ = d / 2 = r Sen (β / 2), de unde există o relație pentru a găsi lungimea d pe latura unui poligon cunoscut raza acestuia r și unghiul său central β:
d = 2 r Sen (β / 2)
În cazul heptadecagonului β = 360º / 17 deci tu ai:
d = 2 r Sen (180º / 17) ≈ 0,3675 r
În cele din urmă, se obține formula perimetrului heptadecagonului, cunoscută raza acestuia:
P = 34 r Sen (180º / 17) ≈ 6,2475 r
Perimetrul unui heptadecagon este apropiat de perimetrul circumferinței care îl înconjoară, dar valoarea sa este mai mică, adică perimetrul cercului circumscris este Pcir = 2π r ≈ 6.2832 r.
Zonă
Pentru a determina aria heptadecagonului ne vom referi la figura 2, care arată laturile și apotema unui poligon regulat de n laturile. În această figură triunghiul EOD are o suprafață egală cu baza d (partea poligonului) ori înălțimea la (apotema poligonului) se împarte la Două:
Zona EOD = (d x a) / 2
Atât de cunoscută apotema la a heptadecagonului și a lateralei d aria sa este:
Suprafața heptadecagonului = (17/2) (d x a)
Zona dată lateral
Pentru a obține o formulă pentru aria heptadecagonului cunoscând lungimea celor șaptesprezece laturi ale acestuia, este necesar să se obțină o relație între lungimea apotemului la și lateral d.
Cu referire la figura 2, se obține următoarea relație trigonometrică:
Tan (β / 2) = EJ / OJ = (d / 2) / a, fiind β spre unghiul central CĂPRIOARĂ. Deci apotema la poate fi calculat dacă lungimea este cunoscută d din partea poligonului și a unghiului central β:
a = (d / 2) Cotan (β / 2)
Dacă această expresie este înlocuită acum cu apotema, în formula pentru aria heptadecagonului obținută în secțiunea anterioară, avem:
Zona heptadecagonului = (17/4) (dDouă) Cotan (β / 2)
Fiind β = 360º / 17 pentru heptadecagon, deci avem în sfârșit formula dorită:
Zona heptadecagonului = (17/4) (dDouă) Cotan (180º / 17)
Zona dată de raza
În secțiunile anterioare, a fost găsită o relație între latura d a unui poligon regulat și raza sa r, această relație fiind următoarea:
d = 2 r Sen (β / 2)
Această expresie pentru d este introdus în expresia obținută în secțiunea anterioară pentru zonă. Dacă se fac substituțiile și simplificările pertinente, se obține formula care permite calcularea ariei heptadecagonului:
Zona heptadecagonului = (17/2) (rDouă) Sen (β) = (17/2) (rDouă) Sen (360º / 17)
O expresie aproximativă pentru zonă este:
Suprafața heptadecagonului = 3.0706 (rDouă)
După cum era de așteptat, această zonă este puțin mai mică decât aria cercului care circumscrie heptadecagonul. LAcirc = π rDouă ≈ 3,1416 rDouă. Pentru a fi precis, este cu 2% mai puțin decât cel al cercului său circumscris.
Exemple
Exemplul 1
Pentru ca un heptadecagon să aibă laturi de 2 cm, ce valoare trebuie să aibă raza și diametrul circumferinței circumscrise? Găsiți și valoarea perimetrului.
Pentru a răspunde la întrebare, este necesar să ne amintim de relația dintre latură și raza unui poligon normal cu față n:
d = 2 r Sen (180º / n)
Pentru heptadecagon n = 17, astfel încât d = 0,3675 r, adică raza heptadecagonului este r = 2 cm / 0,3675 = 5,4423 cm sau
10.8844 cm diametru.
Perimetrul unui heptadecagon lateral de 2 cm este P = 17 * 2 cm = 34 cm.
Exemplul 2
Care este aria unui heptadecagon obișnuit cu o latură de 2 cm?
Trebuie să ne referim la formula prezentată în secțiunea anterioară, care ne permite să găsim aria unui heptadecagon când are lungimea d pe partea ta:
Zona heptadecagonului = (17/4) (dDouă) / Tan (180º / 17)
La substituire d = 2 cm în formula de mai sus obțineți:
Zonă = 90,94 cm
Referințe
- C. E. A. (2003). Elemente de geometrie: cu exerciții și geometria busolei. Universitatea din Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematică 2. Grupo Editorial Patria.
- Eliberat, K. (2007). Descoperiți poligoanele. Benchmark Education Company.
- Hendrik, V. (2013). Poligoane generalizate. Birkhäuser.
- IGER. (s.f.). Matematică Primul semestru Tacaná. IGER.
- Jr. geometrie. (2014). Poligoane. Lulu Press, Inc..
- Miller, Heeren și Hornsby. (2006). Matematică: raționament și aplicații (ediția a zecea). Pearson Education.
- Patiño, M. (2006). Matematică 5. Editorial Progreso.
- Sada, M. Poligon regulat pe 17 fețe cu riglă și busolă. Recuperat de pe: geogebra.org
- Wikipedia. Heptadecagon. Recuperat de pe: es.wikipedia.com



Nimeni nu a comentat acest articol încă.