homoscedasticitate într-un model statistic predictiv apare dacă în toate grupurile de date ale uneia sau mai multor observații, varianța modelului în raport cu variabilele explicative (sau independente) rămâne constantă.
Un model de regresie poate fi homoscedastic sau nu, caz în care vorbim heteroscedasticitate.
Un model de regresie statistică a mai multor variabile independente se numește homoscedastic, numai dacă varianța erorii variabilei prezise (sau abaterea standard a variabilei dependente) rămâne uniformă pentru diferite grupuri valori ale variabilelor explicative sau independente.
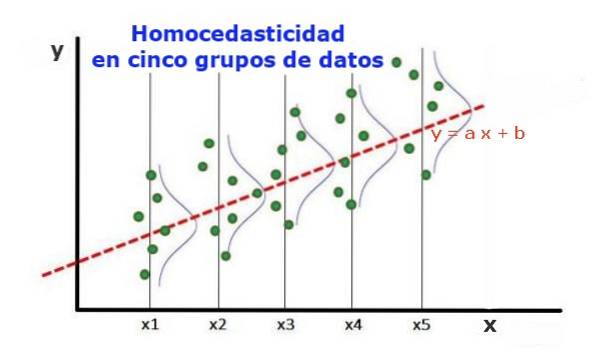
În cele cinci grupuri de date din Figura 1, a fost calculată varianța în fiecare grup, în raport cu valoarea estimată de regresie, rezultând să fie aceeași în fiecare grup. Se presupune în continuare că datele respectă distribuția normală.
La nivel grafic, înseamnă că punctele sunt împrăștiate în mod egal sau împrăștiate în jurul valorii prezise de ajustarea de regresie și că modelul de regresie are aceeași eroare și valabilitate pentru intervalul variabilei explicative..
Indice articol
Pentru a ilustra importanța homoscedasticității în statisticile predictive, este necesar să contrastăm cu fenomenul opus, heteroscedasticitatea.
În cazul figurii 1, în care există omoscedasticitate, este adevărat că:
Var ((y1-Y1); X1) ≈ Var ((y2-Y2); X2) ≈ ... Var ((y4-Y4); X4)
În cazul în care Var ((yi-Yi); Xi) reprezintă varianța, perechea (xi, yi) reprezintă date din grupul i, în timp ce Yi este valoarea prezisă de regresie pentru valoarea medie Xi a grupului. Varianța celor n date din grupul i se calculează după cum urmează:
Var ((yi-Yi); Xi) = ∑j (yij - Yi) ^ 2 / n
Dimpotrivă, atunci când apare heteroscedasticitatea, este posibil ca modelul de regresie să nu fie valid pentru întreaga regiune în care a fost calculat. Figura 2 prezintă un exemplu al acestei situații.
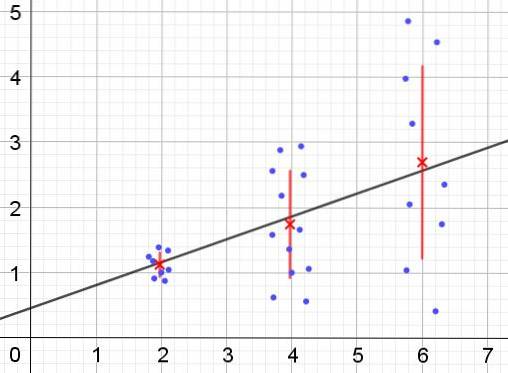
Figura 2 reprezintă trei grupuri de date și potrivirea setului folosind o regresie liniară. Trebuie remarcat faptul că datele din al doilea și al treilea grup sunt mai dispersate decât în primul grup. Graficul din figura 2 arată, de asemenea, valoarea medie a fiecărui grup și bara de eroare a acestuia ± σ, cu deviația standard σ a fiecărui grup de date. Trebuie amintit că abaterea standard σ este rădăcina pătrată a varianței.
Este clar că, în cazul heteroscedasticității, eroarea de estimare a regresiei se schimbă în intervalul de valori ale variabilei explicative sau independente, iar în intervalele în care această eroare este foarte mare, predicția de regresie nu este fiabilă sau nu se aplică.
Într-un model de regresie, erorile sau reziduurile (și -Y) trebuie distribuite cu varianță egală (σ ^ 2) pe parcursul intervalului de valori ale variabilei independente. Din acest motiv, un bun model de regresie (liniar sau neliniar) trebuie să treacă testul de homoscedasticitate..
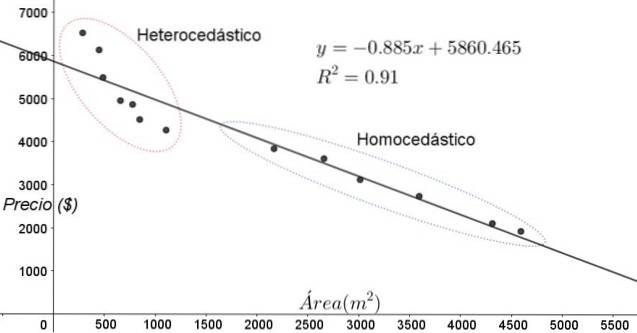
Punctele prezentate în figura 3 corespund datelor unui studiu care caută o relație între prețurile (în dolari) ale caselor în funcție de mărimea sau suprafața în metri pătrați.
Primul model care trebuie testat este cel al unei regresii liniare. În primul rând, se observă că coeficientul de determinare R ^ 2 al ajustării este destul de ridicat (91%), deci se poate crede că ajustarea este satisfăcătoare..
Cu toate acestea, două regiuni se pot distinge clar de graficul de ajustare. Una dintre ele, cea din dreapta închisă într-un oval, îndeplinește homoscedasticitatea, în timp ce regiunea din stânga nu are homoscedasticitate.
Aceasta înseamnă că predicția modelului de regresie este adecvată și fiabilă în intervalul cuprins între 1800 m ^ 2 și 4800 m ^ 2, dar foarte inadecvată în afara acestei regiuni. În zona heteroscedastică, eroarea nu numai că este foarte mare, dar și datele par să urmeze o tendință diferită de cea propusă de modelul de regresie liniară..
Graficul de dispersie al datelor este cel mai simplu și mai vizual test al homoscedasticității lor, cu toate acestea, în ocaziile în care nu este la fel de evident ca în exemplul prezentat în figura 3, este necesar să recurgeți la grafice cu variabile auxiliare..
Pentru a separa zonele în care homoscedasticitatea este îndeplinită și unde nu este, sunt introduse variabilele standardizate ZRes și ZPred:
ZRes = Abs (y - Y) / σ
ZPred = Y / σ
Trebuie remarcat faptul că aceste variabile depind de modelul de regresie aplicat, deoarece Y este valoarea predicției de regresie. Mai jos este graficul scatter ZRes vs ZPred pentru același exemplu:
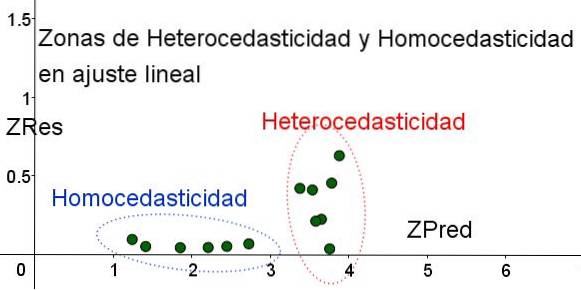
În graficul din Figura 4 cu variabilele standardizate, aria în care eroarea reziduală este mică și uniformă este clar separată de zona în care nu este. În prima zonă, homoscedasticitatea este îndeplinită, în timp ce în regiunea în care eroarea reziduală este foarte variabilă și mare, heteroscedasticitatea este îndeplinită..
Reglarea regresiei se aplică aceluiași grup de date din figura 3, în acest caz ajustarea este neliniară, deoarece modelul utilizat implică o funcție potențială. Rezultatul este prezentat în figura următoare:
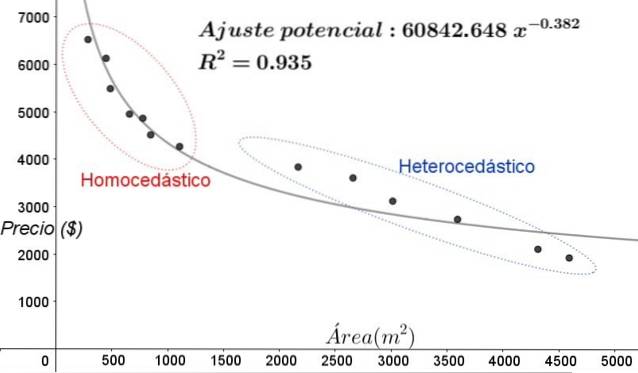
În graficul din Figura 5, zonele homoscedastice și heteroscedastice ar trebui notate clar. De asemenea, trebuie remarcat faptul că aceste zone au fost schimbate față de cele care au fost formate în modelul de potrivire liniară.
În graficul din figura 5 este evident că, chiar și atunci când există un coeficient destul de mare de determinare a ajustării (93,5%), modelul nu este adecvat pentru întregul interval al variabilei explicative, deoarece datele pentru valori mai mari de 2000 m ^ 2 prezintă heteroscedasticitate.
Unul dintre testele non-grafice cel mai utilizat pentru a verifica dacă homoscedasticitatea este îndeplinită sau nu este Test Breusch-Pagan.
Nu toate detaliile acestui test vor fi date în acest articol, dar caracteristicile sale fundamentale și pașii acestuia sunt prezentate în linii mari:
Majoritatea pachetelor software statistice precum: SPSS, MiniTab, R, Python Pandas, SAS, StatGraphic și altele încorporează testul de homoscedasticitate a Breusch-Pagan. Un alt test pentru a verifica uniformitatea varianței Testul Levene.
Nimeni nu a comentat acest articol încă.