Identități trigonometrice (exemple și exerciții)

identități trigonometrice sunt relații între rapoarte trigonometrice, care sunt adevărate pentru orice valoare a variabilei. De exemplu:

tan θ = sin θ / cos θ

Este o identitate trigonometrică care raportează trei rapoarte ale unghiului θ, tangentei, sinusului și cosinusului respectivului unghi.

Această identitate este adevărată pentru toate valorile, cu excepția celor care fac din numitorul 0. Cos θ este 0 pentru θ = ± π / 2, ± 3π / 2, ± 5π / 2 ... Un alt exemplu de identitate trigonometrică este:

păcat x. sec x. ctg x = 1

Indice articol

• 1 Demo
• 2 Tipuri de identități trigonometrice
  • 2.1 - Identități trigonometrice fundamentale
  • 2.2 - Identități pitagoreice
  • 2.3 - Formule pentru cosinus și sinus pentru adunarea / scăderea unghiurilor
  • 2.4 - Formule pentru unghiul dublu
  • 2.5 - Formule pentru jumătatea unghiului
• 3 exerciții rezolvate
  • 3.1 - Exercițiul 1
  • 3.2 - Exercițiul 2
• 4 Referințe

Demonstrație

Există două moduri de bază de a arăta că o identitate trigonometrică este adevărată:

1- Transformarea unuia dintre membrii egalității în celălalt, prin manipulări algebrice convenabile.

2- Dezvoltați ambii membri ai egalității separat, până când expresiile finale respective ale fiecăruia sunt exact aceleași.

În identitatea propusă, vom transforma partea stângă a egalității, pentru care exprimăm ctg x și sec x în termeni de sinus și cosinus după cum urmează:

ctg x = cos x / sin x

sec x = 1 / cos x

Înlocuim această expresie din partea stângă a identității și simplificăm:

păcat x. (1 / cos x). (cos x / sin x) = (sin x. cos x / cos x. sin x) = 1

Iar veridicitatea identității este deja verificată.

Tipuri de identități trigonometrice

Există mai multe clase de identități trigonometrice. Vom descrie pe scurt principalele de mai jos:

- Identități trigonometrice fundamentale

Distingem două tipuri de identități fundamentale:

I) Cele care sunt exprimate prin raporturile de bază sinus, cosinus și tangent:

• sec x = 1 / cos x
• cosec x / 1 / sin x
• ctg x = 1 / tg x
• tg x = sin x / cos x
• ctg x = cos x / sin x

II) Cele derivate din paritate. Știm din graficul său că sin x este o funcție ciudată, ceea ce înseamnă că:

sin (-x) = - sin x

La rândul său, cos x este o funcție uniformă, prin urmare:

cos (-x) = cos x

Atunci:

tg (-x) = sin (-x) / cos (-x) = -sen x / cos x

În mod similar:

• cotg (-x) = -ctg x
• sec (-x) = sec x
• cosec (-x) = - cosec x

- Identități pitagoreice

Acestea se obțin din aplicarea teoremei pitagoreice la triunghiul dreptunghiular al picioarelor a și b și hipotenuzei c. Sa vedem:

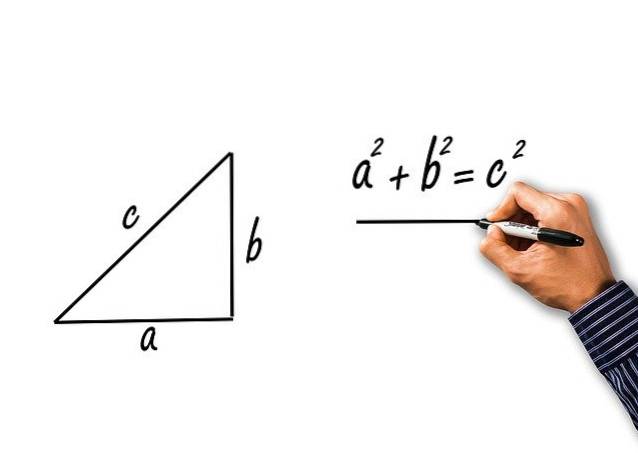
Teorema lui Pitagora afirmă că:

c^Două = a^Două + b^Două

Împărțind totul prin c^Două:

c^Două / c^Două = (a^Două / c^Două) + (B^Două / c^Două)

Termenul din stânga este 1 și ne amintim că sinusul și cosinusul unghiului acut α sunt definite ca:

sin α = a / c

cos α = b / c

Rezultat:

1 = (sin α)^Două + (cos α)^Două

Această identitate este cunoscută sub numele de identitate fundamentală.

Procedura poate fi efectuată prin împărțirea la a^Două și b^Două, ceea ce dă naștere la încă două identități:

sec^Două α = 1 + tg^Două α

recolta^Două α = 1 + ctg^Două α

- Formule pentru cosinus și sinus pentru adunarea / scăderea unghiurilor

Principalele identități trigonometrice pentru cosinus, sinus și tangentă de adunare și scădere sunt după cum urmează:

Dovada păcatului (α + β) și a cos (α + β)

Aceste identități pot fi dovedite geometric sau, de asemenea, prin formula lui Euler:

și^iα = cos α + i sin α

Să vedem ce se întâmplă cu formula atunci când se substituie suma a două unghiuri α și β:

și^{i (α +β)} = cos (α + β) + i sin (α + β)

Această expresie este complexă, partea sa reală este cos (α + β), iar partea sa imaginară este i sin (α + β). Salvăm acest rezultat pentru o utilizare ulterioară și ne concentrăm pe dezvoltarea părții exponențiale:

și^{i (α +β)} = e^iα ⋅ e^iβ = (cos α + i sin α). (cos β + i sin β) =

= cos α⋅cos β + cos α⋅i sin β + i⋅sen α cos β - sin α⋅sen β

Partea reală a acestei expresii este cea care nu este înmulțită cu unitatea imaginară „i”:

cos α⋅cos β - sin α. păcatul β

Prin urmare, partea imaginară este:

i (cos α⋅sen β + sin α⋅cos β)

Pentru ca două expresii complexe să fie egale, partea reală a uneia trebuie să fie egală cu partea reală a celeilalte. La fel se întâmplă și cu părțile imaginare.

Luăm rezultatul salvat și îl comparăm cu acesta:

cos α. cos β - sin α. sin β = cos (α + β)

i (cos α⋅sen β + sin α⋅cos β) = i sin (α + β)

sin (α + β) = (cos α. sin β + sin α⋅cos β)

- Formule pentru unghiul dublu

În formulele anterioare luăm β = α și dezvoltăm:

sin (α + α) = sin 2 α = sin α⋅cos α + cos α. sin α = 2⋅ sin α ⋅ cos α

cos (α + α) = cos 2 α = cos α⋅cos α - sin α⋅sen α = cos^Două α - păcat ^Două α

tg (α + α) = tg 2 α = [tg α + tg α] / [1- tg α⋅tg α] = 2tg α / 1- tg^Două α

Dacă în a doua expresie înlocuim cos^Două α = 1 - păcat^Două α se obține:

cos 2 α = cos^Două α - (1- cos^Două α) = 2 cos^Două α -1

- Formule pentru jumătatea unghiului

În această ultimă expresie, să substituim α cu α / 2, rămân următoarele:

cos α = 2 cos ^Două(a / 2) -1

Rezolvarea pentru:

Exerciții rezolvate

- Exercitiul 1

Arata asta:

Vom lucra termenul stâng algebric, astfel încât să arate ca cel potrivit. Deoarece păcatul x apare la termenul potrivit, primul pas este să exprimăm cos^Douăx în termeni de păcat x astfel încât totul să fie în termeni de același raport trigonometric:

Apoi 1 - păcatul este luat în considerare^Două x pentru că este o diferență de pătrate perfecte. Pentru a face acest lucru, șterge identitatea fundamentală:

cos^Douăx = 1 - păcat^Două X

1 - sen^Două x = (1- sin x) (1 + sinx)

Și factorizarea este substituită în expresia originală:

Termenul (1- sinx) este simplificat și rămâne o egalitate:

1 + sin x = 1 + sinx

- Exercițiul 2

Rezolvați următoarea ecuație trigonometrică și dați soluția pentru valori cuprinse între 0 și 360º:

tg x + sec^Două x = 3

Soluţie

În termenul din stânga există două rapoarte trigonometrice, de aceea este necesar să se reducă totul la unul singur, pentru a putea rezolva necunoscutul. Termenul sec^Două x se exprimă printr-una dintre identitățile pitagoreice:

sec^Două α = 1 + tg^Două α

Înlocuirea în ecuație rămâne:

tg x + 1 + tg^Două x = 3

Rearanjarea termenilor:

tg^Două x + tg x + 1 = 3

Această ecuație este rezolvată prin schimbarea variabilei:

tg x = u

sau^Două + u + 1 - 3 = 0 → u^Două + u - 2 = 0

Această ecuație pătratică este ușor rezolvată prin factorizarea:

(u +2) (u-1) = 0

Prin urmare u₁ = -2 și u_Două = 1, care este echivalent cu:

tg x₁ = -2

tg x_Două = 1

In cele din urma:

X₁ = arctg (-2) = 296,6º

X_Două  = arctg (1) = 45º

Referințe

1. Carena, M. 2019. Manual pre-universitar de matematică. Universitatea Națională a Litoralului.
2. Figuera, J. 1999. Matematică. Primul. Diversificat. Ediții colegiale bolivariene.
3. Hoffman, J. Selecția subiectelor de matematică. Volumul 4.
4. Jiménez, R. 2008. Algebra. Prentice hall.
5. Wikipedia. Identități și formule de trigonometrie. Recuperat de pe: es.wikipedia.org.
6. Zapata, F. 4 moduri de a rezolva o ecuație pătratică. Recuperat de pe: francesphysics.blogspot.com.
7. Zill, D. 1984. Algebră și trigonometrie. Dealul Mcgraw.