Cele 10 caracteristici principale ale pieței

Caracteristica pătratului principal este faptul că este alcătuită din patru laturi, care au exact aceleași măsurători. Aceste laturi sunt aranjate pentru a forma patru unghiuri drepte (90 °).

pătrat Este o figură geometrică de bază, obiect de studiu al geometriei plane, deoarece este o figură bidimensională (care are lățime și înălțime, dar nu are adâncime).

Pătratele sunt poligoane. Mai precis, poligoanele sunt (a) patrulatere, deoarece au patru laturi, (b) echilaterale, deoarece au laturi care măsoară la fel, și (c) echiangle, deoarece au unghiuri cu aceeași amplitudine..

Aceste ultime două proprietăți ale pătratului (echilateral și echiangular) pot fi rezumate într-un singur cuvânt: regulat. Aceasta înseamnă că pătratele sunt poligoane patrulatere regulate.

La fel ca alte figuri geometrice, pătratul are o suprafață. Acest lucru poate fi calculat prin înmulțirea uneia dintre laturile sale cu ea însăși. De exemplu, dacă avem un pătrat care măsoară 4 mm, aria acestuia ar fi de 16 mm^Două.

Pătrate Caracteristici remarcabile

1- Numărul laturilor și dimensiunea

Pătratele sunt formate din patru laturi care măsoară la fel. De asemenea, pătratele sunt figuri bidimensionale, ceea ce înseamnă că au doar două dimensiuni: lățime și înălțime..

Caracteristica de bază a pătratelor este că au patru laturi. Sunt figuri plate, deci sunt numite bidimensionale.

2- Poligon

Pătratele sunt un poligon. Aceasta înseamnă că pătratele sunt figuri geometrice delimitate de o linie închisă formată din segmente de linie consecutive (linie poligonală închisă).

Mai exact, este un poligon patrulater, deoarece are patru laturi.

3- poligon echilateral

Se spune că un poligon este echilateral atunci când toate părțile au aceeași măsură. Aceasta înseamnă că, dacă una dintre laturile pătratului măsoară 2 metri, toate laturile vor măsura doi metri..

Pătratele sunt echilaterale, ceea ce înseamnă că toate laturile lor măsoară la fel.

În imagine, este afișat un pătrat cu laturile egale de 5 cm.

4- Poligon echiangular

Se spune că un poligon este echiangular atunci când toate unghiurile formate de linia poligonală închisă au aceeași măsură.

Toate pătratele sunt alcătuite din patru unghiuri drepte (adică unghiuri de 90 °), indiferent de măsurătorile particulare ale unghiului: atât un pătrat de 2 cm x 2 cm, cât și un pătrat de 10 m x 10 m au patru unghiuri drepte.

Toate pătratele sunt egale, deoarece unghiurile lor au aceeași amplitudine. Adică 90 °.

5- Poligon regulat

Când un poligon este atât echilateral, cât și echiangular, este considerat a fi un poligon regulat.

Deoarece pătratul are laturi care măsoară același și unghiuri de amplitudine egală, se poate spune că acesta este un poligon regulat.

Pătratele au ambele laturi de măsură egală și unghiuri de lățime egală, deci sunt poligoane regulate.

În imaginea de mai sus, este afișat un pătrat cu patru laturi de 5 cm și patru unghiuri de 90 °.

6- Suprafața unui pătrat

Suprafața unui pătrat este egală cu produsul unei fețe și a celeilalte fețe. Deoarece cele două laturi au exact aceeași măsură, formula poate fi simplificată spunând că aria acestui poligon este egală cu una dintre laturile sale pătrate, adică (latură)^Două.

Câteva exemple de calcul al ariei unui pătrat sunt:

- Pătrat cu laturile de 2 m: 2 m x 2 m = 4 m^Două

- Patratele cu laturile de 52 cm: 52 cm x 52 cm = 2704 cm^Două

- Pătrat cu laturile de 10 mm: 10 mm x 10 mm = 100 mm^Două

Pătratul prezentat în imagine are laturile de 5 cm.

Suprafața sa va fi produsul de 5 cm x 5 cm, sau ceea ce este același (5cm)^Două

În acest caz, suprafața pătratului este de 25 cm^Două

7- Pătratele sunt paralelograme

Paralelogramele sunt un tip de patrulater care are două perechi de laturi paralele. Aceasta înseamnă că o pereche de părți se confruntă una cu cealaltă, în timp ce același lucru se întâmplă cu cealaltă pereche..

Există patru tipuri de paralelograme: dreptunghiuri, romburi, romboizi și pătrate..

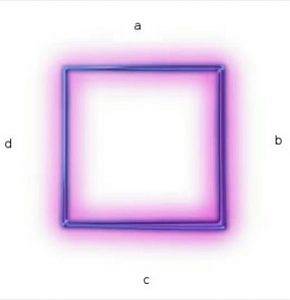
Pătratele sunt paralelograme, deoarece au două perechi de laturi care sunt paralele..

Laturile (a) și (c) sunt paralele.

Partile (b) și (d) sunt paralele.

8- Unghiurile opuse sunt congruente, iar cele consecutive sunt complementare

Că două unghiuri sunt congruente înseamnă că au aceeași amplitudine. În acest sens, întrucât un pătrat are toate unghiurile de aceeași amplitudine, se poate spune că unghiurile opuse sunt congruente.

Pe de altă parte, faptul că două unghiuri consecutive sunt complementare înseamnă că suma acestor două este egală cu un unghi drept (cel care are o amplitudine de 180 °).

Unghiurile unui pătrat sunt unghiuri drepte (90 °), deci suma lor dă 180 °.

9- Sunt construite dintr-o circumferință

Pentru a construi un pătrat, se desenează un cerc. Ulterior, pe această circumferință sunt trasate două diametre; aceste diametre trebuie să fie perpendiculare, formând o cruce.

Odată ce diametrele au fost trase, vom avea patru puncte în care segmentele de linie intersectează circumferința. Dacă aceste patru puncte sunt unite, rezultatul este un pătrat.

10- Diagonalele se intersectează în punctul lor mediu

Diagonalele sunt linii drepte care sunt trasate dintr-un unghi în altul opus. Într-un pătrat, pot fi desenate două diagonale. Aceste diagonale se vor intersecta în mijlocul pătratului.

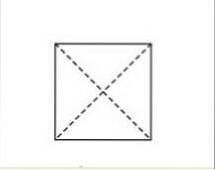
În imagine, liniile punctate reprezintă diagonalele. După cum puteți vedea, aceste linii se intersectează exact în mijlocul pătratului..

Referințe

1. Pătrat. Adus la 17 iulie 2017, de pe en.wikipedia.org
2. Piața și proprietățile sale. Adus pe 17 iulie 2017, de pe mathonpenref.com
3. Proprietățile romburilor, dreptunghiurilor și pătratelor. Adus pe 17 iulie 2017, de pe dummies.com
4. Proprietățile unui pătrat. Adus pe 17 iulie 2017, de pe coolmth.com
5. Pătrat. Adus pe 17 iulie 2017, de pe onlinemschool.com
6. Proprietățile pătratelor. Adus la 17 iulie 2017, de pe brlliant.org.