Legea Coulomb legea fizică este cea care guvernează interacțiunea dintre obiectele încărcate electric. A fost enunțată de omul de știință francez Charles Augustin de Coulomb (1736-1806), grație rezultatelor experimentelor sale folosind balanța de torsiune.
În 1785, Coulomb a experimentat de nenumărate ori cu sfere mici încărcate electric, de exemplu mutând două sfere mai aproape sau mai departe, variind magnitudinea sarcinii și, de asemenea, semnul lor. Observați și înregistrați întotdeauna cu atenție fiecare răspuns.
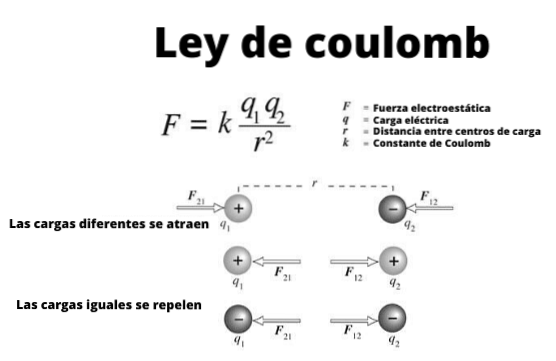
Aceste sfere mici pot fi considerate ca fiind sarcini punctuale, adică obiecte ale căror dimensiuni sunt nesemnificative. Și împlinesc, așa cum se știa încă din vremea vechilor greci, că acuzațiile aceluiași semn se resping și atrag cele ale unui semn diferit..
Având în vedere acest lucru, Charles Coulomb a găsit următoarele:
-Forța atractivă sau respingătoare dintre încărcăturile în două puncte este direct proporțională cu produsul mărimii sarcinilor.
-Această forță este întotdeauna îndreptată de-a lungul liniei care unește sarcinile.
-În cele din urmă, magnitudinea forței este invers proporțională cu pătratul distanței dintre sarcini.
Indice articol
Datorită acestor observații, Coulomb a concluzionat că magnitudinea forței F între două acuzații punctuale ce1 Da ceDouă, a separat o distanță r, este dat matematic ca:
Deoarece forța este o mărime vectorială, pentru a o exprima complet se definește un vector unitate r în direcția liniei care unește sarcinile (un vector unitar are magnitudine egală cu 1).
În plus, constanta de proporționalitate necesară pentru a transforma expresia anterioară într-o egalitate se numește kși sau pur și simplu k: the constanta electrostatică sau Constanta lui Coulomb.
În cele din urmă, legea lui Coulomb este stabilită pentru taxele punctuale, date de:
Forța, ca întotdeauna în sistemul internațional de unități, vine în newton (N). În ceea ce privește taxele, unitatea este numită coulomb (C) în onoarea lui Charles Coulomb și, în cele din urmă, distanța r vine în metri (m).
Privind cu atenție ecuația de mai sus, este clar că constanta electrostatică trebuie să aibă unități de N.mDouă / CDouă, pentru a obține newtoni ca urmare. Valoarea constantei a fost determinată experimental ca:
kși = 8,89 x 10 9 N.mDouă / CDouă ≈ 9 x 10 9 N.mDouă / CDouă
Figura 1 ilustrează interacțiunea dintre două încărcături electrice: atunci când au același semn, se resping, altfel atrag.
Rețineți că legea lui Coulomb se conformează celei de-a treia legi a lui Newton sau legea de acțiune și reacție, deci mărimile lui F1 Da FDouă sunt aceleași, direcția este aceeași, dar simțurile sunt opuse.
Pentru a rezolva problemele interacțiunilor dintre sarcinile electrice, trebuie să se țină seama de următoarele:
- Ecuația se aplică exclusiv în cazul sarcinilor punctuale, adică a obiectelor încărcate electric, dar de dimensiuni foarte mici. Dacă obiectele încărcate au dimensiuni măsurabile, este necesar să le împărțiți în sarcini foarte mici și apoi să adăugați contribuțiile fiecăreia dintre aceste sarcini, pentru care este necesar un calcul integral..
- Forța electrică este o mărime vectorială. Dacă există mai mult de două sarcini interacționale, forța netă asupra sarcinii qeu este dat de principiul suprapunerii:
Fnet = Fi1 + Fi2 + Fi3 + Fi4 +… = ∑ Fij
Unde indicele j este egal cu 1, 2, 3, 4 ... și reprezintă fiecare dintre sarcinile rămase.
- Ar trebui să fiți întotdeauna în concordanță cu unitățile. Cel mai frecvent lucru este să lucrați cu constanta electrostatică în unitățile SI, atunci este necesar să vă asigurați că încărcăturile sunt în coulombi și distanțele în metri.
- În cele din urmă, ecuația se aplică atunci când sarcinile sunt în echilibru static.
În figura următoare există două sarcini punctuale + q și + 2q. Un al treilea punct de încărcare -q este plasat la P. Se cere să se găsească forța electrică pe această încărcare datorită prezenței celorlalte.
Primul lucru este de a stabili un sistem de referință adecvat, care în acest caz este axa orizontală sau axa x. Originea unui astfel de sistem poate fi oriunde, dar pentru comoditate va fi plasat la P, așa cum se arată în figura 4a:
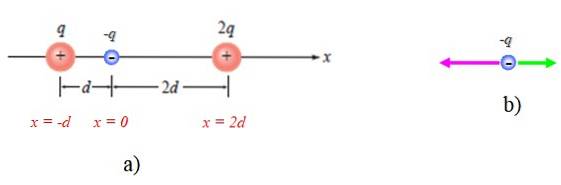
De asemenea, este prezentată o diagramă a forțelor pe -q, luând în considerare faptul că este atrasă de celelalte două (figura 4b).
Hai sa sunăm F1 forța exercitată de sarcina q asupra sarcinii -q, sunt îndreptate de-a lungul axei x și indică direcția negativă, prin urmare:
În mod analog, se calculează FDouă:
Rețineți că magnitudinea FDouă este jumătate din cea a F1, deși sarcina este dublă. Pentru a găsi forța netă, în cele din urmă acestea sunt adăugate vectorial F1 Da FDouă:
Fnet = (-k + k / 2). (qDouă / dDouă) (X) N = - (k / 2). (QDouă / dDouă) (X) N
Două bile de polistiren cu masă egală m = 9,0 x 10-8 kg au aceeași sarcină pozitivă Q și sunt suspendate de un fir de mătase de lungime L = 0,98 m. Sferele sunt separate de o distanță de d = 2 cm. Calculați valoarea lui Q.
Situația declarației este descrisă în figura 5a.
Alegem una dintre sfere și pe aceasta desenăm schema de corp izolată, care include trei forțe: greutatea W, tensiune în frânghie T și repulsie electrostatică F, așa cum apare în figura 5b. Și acum pașii:
Valoarea lui θ / 2 se calculează cu triunghiul din figura 5c:
θ / 2 = arcsen (1 x 10-Două/0,98) = 0,585º
Apoi trebuie să aplicăm a doua lege a lui Newton și să o setăm egală cu 0, deoarece sarcinile sunt în echilibru static. Important, tensiunea T este înclinat și are două componente:
∑FX = -T.sin θ + F = 0
∑FDa = T.cos θ - W = 0
Rezolvăm magnitudinea stresului din ultima ecuație:
T = W / cos θ = mg / cos θ
Această valoare este înlocuită în prima ecuație pentru a găsi magnitudinea lui F:
F = T sin θ = mg (sin θ / cos θ) = mg. tg θ
Deoarece F = k QDouă / dDouă, șterge Q:
Q = 2 × 10-unsprezece C.
Verificarea legii lui Coulomb este ușoară folosind un balans de torsiune similar cu cel folosit de Coulomb în laboratorul său..
Există două sfere mici de soc, dintre care una, cea din centrul balanței, este suspendată de un fir. Experimentul constă în atingerea sferelor de soc descărcate cu o altă sferă metalică încărcată cu încărcare Q.
Imediat încărcătura este distribuită în mod egal între cele două sfere de soc, dar apoi, deoarece sunt sarcini cu același semn, se resping reciproc. O forță acționează asupra sferei suspendate care determină răsucirea firului de care atârnă și se îndepărtează imediat de sfera fixă.
Apoi vedem că oscilează de câteva ori până ajunge la echilibru. Apoi, torsiunea tijei sau a firului care o ține este echilibrată de forța de respingere electrostatică.
Dacă inițial sferele erau la 0º, acum sfera în mișcare va fi rotită un unghi θ. Înconjurând scara, există o bandă gradată în grade pentru a măsura acest unghi. Determinând anterior constanta de torsiune, atunci se calculează cu ușurință forța respingătoare și valoarea sarcinii dobândite de sferele de soc..
Nimeni nu a comentat acest articol încă.