
Caracteristicile liniei perpendiculare, exemple, exerciții
A linie perpendiculară Este unul care formează un unghi de 90 ° față de o altă linie, curbă sau suprafață. Rețineți că atunci când două linii sunt perpendiculare și sunt pe același plan, atunci când se intersectează formează patru unghiuri identice, fiecare de 90º.
Dacă unul dintre unghiuri nu este 90º, se spune că liniile sunt oblice. Liniile perpendiculare sunt comune în proiectare, arhitectură și construcție, de exemplu rețeaua de țevi din imaginea următoare.

Orientarea liniilor perpendiculare poate fi diversă, cum ar fi cele prezentate mai jos:
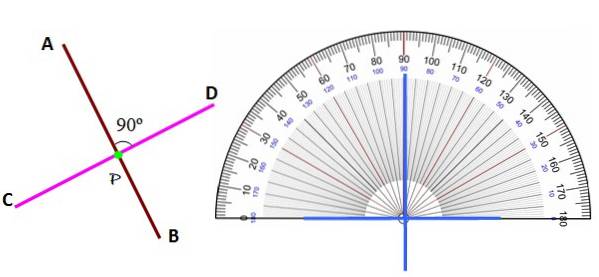
Indiferent de poziție, liniile perpendiculare una pe cealaltă sunt recunoscute prin identificarea unghiului dintre ele ca 90º, cu ajutorul transportorului.
Rețineți că, spre deosebire de liniile paralele din plan, care nu se intersectează niciodată, liniile perpendiculare o fac întotdeauna într-un punct P, numit picior a uneia dintre linii peste cealaltă. Prin urmare sunt și două linii perpendiculare blotere.
Orice linie are perpendiculare infinite, deoarece doar prin deplasarea segmentului AB la stânga sau la dreapta peste segmentul CD, vom avea noi perpendiculare cu un alt picior.
Cu toate acestea, se numește perpendiculară care trece doar prin mijlocul unui segment bisectoare a segmentului respectiv.
Indice articol
- 1 Exemple de linii perpendiculare
- 1.1 Mai multe exemple de linii perpendiculare
- 2 Exerciții
- 2.1 - Exercițiul 1
- 2.2 - Exercițiul 2
- 3 Referințe
Exemple de linii perpendiculare
Liniile perpendiculare sunt comune în peisajul urban. În următoarea imagine (figura 3), au fost evidențiate doar câteva dintre multele linii perpendiculare care pot fi văzute în fațada simplă a acestei clădiri și elementele sale, cum ar fi ușile, canalele, treptele și multe altele:

Lucrul bun este că trei linii perpendiculare între ele ne ajută să stabilim locația punctelor și a obiectelor în spațiu. Acestea sunt axele de coordonate identificate ca Axa X., Axa y Da axa z, vizibil în colțul unei camere dreptunghiulare ca cea de mai jos:
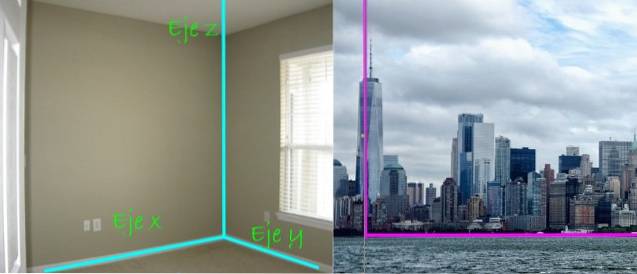
În vederea panoramică a orașului, în dreapta, se observă și perpendicularitatea dintre zgârie-nori și sol. Primul, am spune, se găsește de-a lungul axa z, în timp ce solul este un plan, care în acest caz este planul X y.
Dacă solul constituie planul X y, zgârie-noriul este, de asemenea, perpendicular pe orice bulevard sau stradă, ceea ce garantează stabilitatea acestuia, deoarece o structură înclinată este instabilă.
Și pe străzi, oriunde există colțuri dreptunghiulare, există linii perpendiculare. Multe bulevarde și străzi au un aspect perpendicular, atâta timp cât terenul și caracteristicile geografice o permit..
Pentru a exprima pe scurt perpendicularitatea dintre linii, segmente sau vectori, se utilizează simbolul ⊥. De exemplu, dacă linia L1 este perpendicular pe dreapta LDouă, noi am scris:
L1 ⊥ LDouă
Mai multe exemple de linii perpendiculare
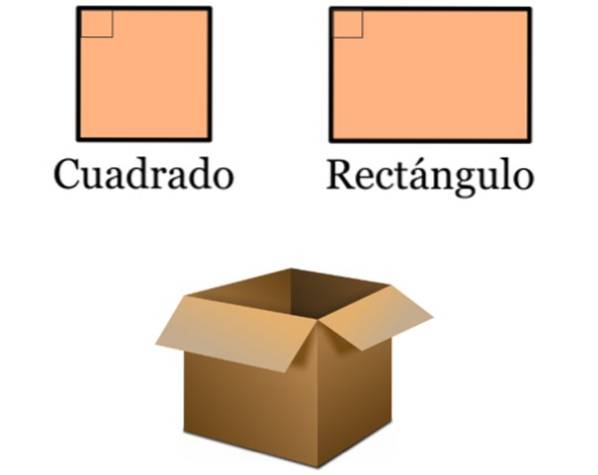
- În proiectare, liniile perpendiculare sunt foarte prezente, deoarece multe obiecte comune se bazează pe pătrate și dreptunghiuri. Aceste patrulatere se caracterizează prin unghiuri interne de 90º, deoarece laturile lor sunt paralele două câte două:
- Domeniile în care se practică diferite sporturi sunt delimitate de numeroase pătrate și dreptunghiuri. Acestea la rândul lor conțin linii perpendiculare.
- Două dintre segmentele care alcătuiesc un triunghi dreptunghiular sunt perpendiculare una pe cealaltă. Acestea sunt numite picioare, în timp ce linia rămasă este numită ipotenuză.
- Liniile vectorului câmpului electric sunt perpendiculare pe suprafața unui conductor în echilibru electrostatic.
- Pentru un conductor încărcat, liniile și suprafețele echipotențiale sunt întotdeauna perpendiculare pe cele ale câmpului electric.
- În sistemele de conducte sau conducte utilizate pentru transportul diferitelor tipuri de fluide, cum ar fi gazele prezentate în Figura 1, coatele cu unghi drept sunt frecvente. Prin urmare, ele formează linii perpendiculare, așa este cazul unei camere de cazan:

Instruire
- Exercitiul 1
Desenați două linii perpendiculare folosind o riglă și busolă.
Soluţie
Este foarte simplu de făcut, urmând acești pași:
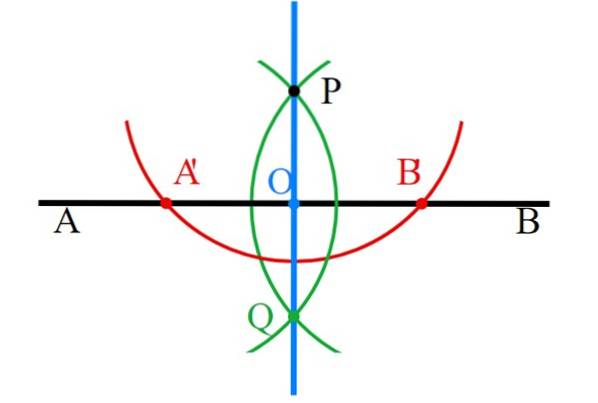
-Se trasează prima linie, numită AB (negru).
-Deasupra (sau dedesubt dacă preferați) marcați punctul AB, prin care va trece perpendicularul. Dacă P este chiar deasupra (sau dedesubt) mijlocului AB, acea perpendiculară este bisectoarea segmentului AB.
-Cu busola centrată pe P, desenați un cerc care taie AB în două puncte, numite A 'și B' (roșu).
-Busola este deschisă la A'P, este centrată pe A 'și se trasează un cerc care trece prin P (verde).
-Repetați pasul anterior, dar deschizând acum măsura lungimea segmentului B'P (verde). Ambele arcuri de circumferință se intersectează în punctul Q sub P și bineînțeles în acesta din urmă.
-Punctele P și Q sunt unite cu rigla și linia perpendiculară (albastră) este gata.
-În cele din urmă, toate construcțiile auxiliare trebuie șterse cu atenție, lăsând doar cele perpendiculare..
- Exercițiul 2
Două linii L1 și euDouă sunt perpendiculare dacă pantele lor respective m1 si mDouă întâlnește această relație:
m1 = -1 / mDouă
Având în vedere linia y = 5x - 2, găsiți o linie perpendiculară pe ea și care trece prin punctul (-1, 3).
Soluţie
-Mai întâi, găsiți panta liniei perpendiculare m⊥, așa cum este indicat în declarație. Panta liniei inițiale este m = 5, coeficientul care însoțește „x”. Atunci:
m⊥= -1/5
-Atunci se construiește ecuația liniei perpendiculare și⊥, înlocuind valoarea găsită anterior:
Da⊥= -1 / 5x + b
-Apoi, se determină valoarea lui b, cu ajutorul punctului dat de enunț, (-1,3), deoarece linia perpendiculară trebuie să treacă prin ea:
y = 3
x = -1
Înlocuind:
3 = -1/5 (-1) + b
Rezolvați pentru valoarea lui b:
b = 3- (1/5) = 14/5
-În cele din urmă se construiește ecuația definitivă:
Da⊥= -1 / 5x + 14/5
Referințe
- Baldor, A. 2004. Geometria planului și a spațiului. Publicații culturale.
- Clemens, S. 2001. Geometrie cu aplicații și rezolvarea problemelor. Addison Wesley.
- Matematica este distractivă. Liniile perpendiculare. Recuperat de pe: mathisfun.com.
- Institutul Monterey. Liniile perpendiculare. Recuperat de pe: montereyinstitute.org.
- Wikipedia. Liniile perpendiculare. Recuperat de pe: es.wikipedia.org.


Nimeni nu a comentat acest articol încă.