
Modelul mecanic cuantic al comportamentului atomului, exemple
model mecanic cuantic al atomului presupune că acesta este format dintr-un nucleu central format din protoni și neutroni. Electronii încărcați negativ înconjoară nucleul în regiuni difuze cunoscute sub numele de orbitali..
Forma și întinderea orbitalilor electronici sunt determinate de diferite magnitudini: potențialul nucleului și nivelurile cuantificate ale energiei și impulsul unghiular al electronilor.
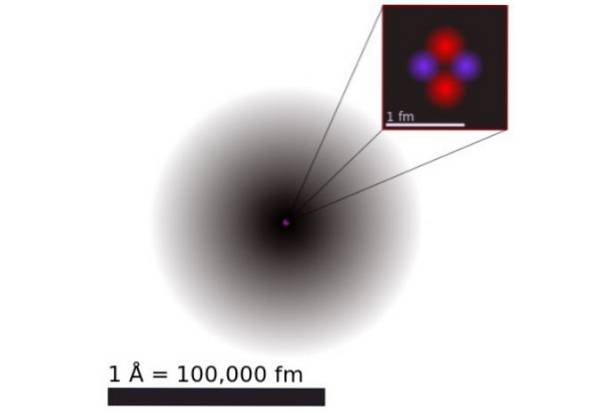
Conform mecanicii cuantice, electronii au comportament dual-undă-particulă și la scara atomică sunt difuzi și non-punctuali. Dimensiunile atomului sunt determinate practic de extensia orbitalilor electronici care înconjoară nucleul pozitiv.
Figura 1 prezintă structura atomului de heliu, care are un nucleu cu doi protoni și doi neutroni. Acest nucleu este înconjurat de norul de probabilitate al celor doi electroni care înconjoară nucleul, care este de o sută de mii de ori mai mic. În imaginea următoare puteți vedea atomul de heliu, cu protonii și neutronii din nucleu și electronii pe orbitali.

Dimensiunea unui atom de heliu este de ordinul unuia angstrom (1 Å), adică 1 x 10 ^ -10 m. În timp ce dimensiunea nucleului său este de ordinul a femtometru (1 fm), adică 1 x 10 ^ -15 m.
În ciuda faptului că este atât de mic, 99,9% din greutatea atomică este concentrată în micul nucleu. Acest lucru se datorează faptului că protonii și neutronii sunt de 2.000 de ori mai grei decât electronii care îi înconjoară..
Indice articol
- 1 Scara atomică și comportamentul cuantic
- 1.1 Primele modele cuantice
- 2 Dinamica undelor materiale
- 2.1 Orbitalii atomici
- 2.2 Numere cuantice
- 3 Forma și dimensiunea orbitalilor
- 3.1 Rotirea
- 4 Referințe
Scara atomică și comportamentul cuantic
Unul dintre conceptele care au avut cea mai mare influență asupra dezvoltării modelului atomic a fost cel al dualității undă - particulă: descoperirea că fiecărui obiect material îi este asociată un val de materie.
Formula pentru calcularea lungimii de undă λ asociat cu un obiect material a fost propus de Louis De Broglie în 1924 și este următorul:
λ = h / (m v)
Unde h este constanta lui Planck, m aluatul și v viteză.
Conform principiului lui De Broglie, fiecare obiect are un comportament dublu, dar în funcție de scara interacțiunilor, viteza și masa, comportamentul undei poate fi mai preeminent decât comportamentul particulelor sau invers..
Electronul este ușor, masa sa este de 9,1 × 10 ^ -31 kg. Viteza tipică a unui electron este de 6000 km / s (de cincizeci de ori mai mică decât viteza luminii). Această viteză corespunde valorilor energetice în intervalul de zeci de electroni volți..
Cu datele de mai sus și utilizând formula de Broglie, lungimea de undă pentru electron poate fi obținută:
λ = 6,6 x 10 ^ -34 J s / (9,1 × 10 ^ -31 kg 6 x 10 ^ 6 m / s) = 1 x 10 ^ -10 m = 1 Å
Electronul la energiile tipice ale nivelurilor atomice, are o lungime de undă de același ordin de mărime ca și cea a scării atomice, astfel încât la acea scară are un comportament de undă și nu o particulă..
Primele modele cuantice
Având în vedere faptul că electronul la scară atomică are un comportament undelor, au fost dezvoltate primele modele atomice bazate pe principiile cuantice. Dintre acestea, se remarcă modelul atomic Bohr, care a prezis perfect spectrul de emisie al hidrogenului, dar nu și cel al altor atomi.
Modelul Bohr și mai târziu modelul Sommerfeld au fost modele semi-clasice. Adică, electronul a fost tratat ca o particulă supusă forței de atracție electrostatică a nucleului care orbita în jurul său, guvernată de a doua lege a lui Newton..
Pe lângă orbitele clasice, aceste prime modele au luat în considerare faptul că electronul avea o undă materială asociată. Doar orbitele al căror perimetru era un număr întreg de lungimi de undă erau permise, deoarece cele care nu îndeplinesc acest criteriu sunt dispărute prin interferențe distructive..
Atunci apare cuantizarea energiei pentru prima dată în structura atomică..
Cuvantul cuantic Tocmai provine din faptul că electronul poate lua doar unele valori de energie discrete în atom. Acest lucru coincide cu descoperirea lui Planck, care a constat în descoperirea că o radiație de frecvență F interacționează cu materia din pachete de energie E = h f, Unde h este constanta lui Planck.
Dinamica undelor materiale
Nu mai exista nicio îndoială că electronul la nivel atomic se comporta ca o undă materială. Următorul pas a fost să găsim ecuația care le guvernează comportamentul. Această ecuație nu este nici mai mult, nici mai puțin decât ecuația Schrodinger, propusă în 1925.
Această ecuație se referă și determină funcția de undă ψ asociat cu o particulă, cum ar fi electronul, cu potențialul său de interacțiune și energia sa totală ȘI. Expresia sa matematică este:


Egalitatea în ecuația Schrodinger este valabilă doar pentru unele valori ale energiei totale ȘI, dând naștere cuantificării energiei. Funcția de undă a electronilor supuși potențialului nucleului este obținută din soluția ecuației Schrodinger.
Orbitalii atomici
Valoarea absolută a funcției de undă pătrată |ψ| ^ 2, oferă amplitudinea probabilității de a găsi electronul într-o poziție dată.
Acest lucru duce la conceptul de orbital, care este definită ca regiunea difuză ocupată de electron cu amplitudine de probabilitate diferită de zero, pentru valorile discrete ale energiei și momentului unghiular determinate de soluțiile ecuației Schrodinger.
Cunoașterea orbitalilor este foarte importantă, deoarece descrie structura atomică, reactivitatea chimică și legăturile posibile pentru a forma molecule.
Atomul de hidrogen este cel mai simplu dintre toți, deoarece are un electron solitar și este singurul care admite o soluție analitică exactă a ecuației Schrodinger.
Acest atom simplu are un nucleu format dintr-un proton, care produce un potențial central de atracție Coulomb care depinde doar de rază. r, deci este un sistem cu simetrie sferică.
Funcția de undă depinde de poziția, dată de coordonatele sferice față de nucleu, deoarece potențialul electric are simetrie centrală.
În plus, funcția de undă poate fi scrisă ca produs al unei funcții care depinde doar de coordonatele radiale și o altă care depinde de coordonatele unghiulare:

Numere cuantice
Soluția ecuației radiale produce valorile discrete ale energiei, care depind de un număr întreg n, numit numărul cuantic principal, care poate lua valori întregi pozitive 1, 2, 3, ...
Valorile energetice discrete sunt valori negative date de următoarea formulă:

Soluția de ecuație unghiulară definește valorile cuantificate ale impulsului unghiular și ale componentei sale z, dând naștere numerelor cuantice l Da ml.
Numărul cuantic al momentului unghiular l merge de la 0 la n-1. Număr cuantic ml se numește numărul cuantic magnetic și pleacă de la -l pana cand +l. De exemplu, da l dacă ar fi 2, numărul cuantic magnetic ar lua valorile -2, -1, 0, 1, 2.
Forma și dimensiunea orbitalilor
Atingerea radială a orbitei este determinată de funcția de undă radila. Este mai mare pe măsură ce energia electronului crește, adică pe măsură ce crește numărul cuantic principal.
Distanța radială este de obicei măsurată în raze Bohr, care pentru cea mai mică energie a hidrogenului este de 5,3 X 10-11 m = 0,53 Å.

Dar forma orbitalilor este determinată de valoarea numărului cuantic al momentului unghiular. Dacă l = 0 avem un orbital sferic numit s, dacă l = 1 avem un orbital lobulat numit p, care poate avea trei orientări în funcție de numărul cuantic magnetic. Următoarea figură arată forma orbitalilor.
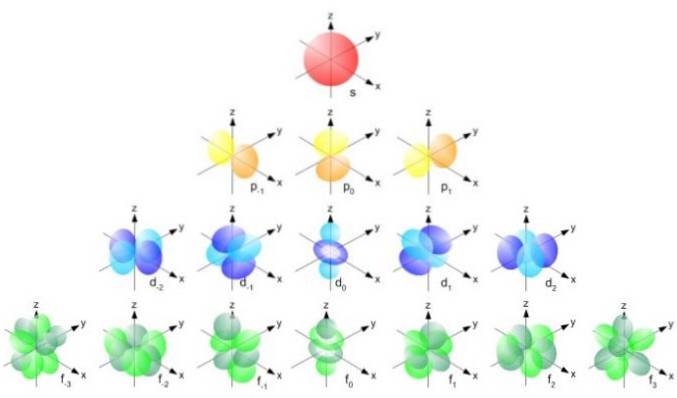
Acești orbitali se împachetează unul în celălalt în funcție de energia electronilor. De exemplu, următoarea figură arată orbitalii dintr-un atom de sodiu.
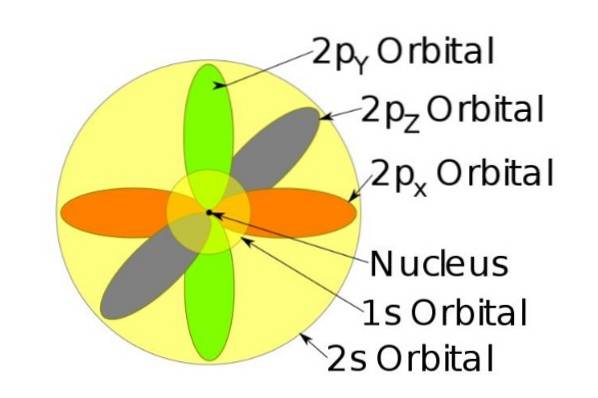
Rotirea
Modelul mecanic cuantic al ecuației Schrödinger nu încorporează rotirea electronului. Dar este luat în considerare prin principiul excluderii Pauli, care indică faptul că orbitalii pot fi populați cu până la doi electroni cu numere cuantice de spin s = + ½ și s = -½.
De exemplu, ionul de sodiu are 10 electroni, adică, dacă ne referim la figura anterioară, există doi electroni pentru fiecare orbital.
Dar dacă este atomul de sodiu neutru, există 11 electroni, dintre care ultimul ar ocupa un orbital 3s (care nu este prezentat în figură și cu o rază mai mare decât 2s). Rotirea atomului este decisivă în caracteristicile magnetice ale unei substanțe.
Referințe
- Alonso - Finn. Fundamente cuantice și statistice. Addison Wesley.
- Eisberg - Resnick. Fizică cuantică. Limusa - Wiley.
- Gasiorowicz. Fizică cuantică. John Wiley & Sons.
- HSC. Curs de fizică 2. Jacaranda plus.
- Wikipedia. Modelul atomic al lui Schrodinger. Recuperat de pe: Wikipedia.com


Nimeni nu a comentat acest articol încă.