Metoda Gauss-Seidel este o procedură iterativă pentru a găsi soluții aproximative la un sistem de ecuații algebrice liniare cu precizie aleasă în mod arbitrar. Metoda se aplică matricilor pătrate cu elemente diferite de zero în diagonalele lor și convergența este garantată dacă matricea este diagonală dominantă.
A fost creată de Carl Friedrich Gauss (1777-1855), care a oferit o demonstrație privată unuia dintre studenții săi în 1823. Ulterior a fost publicată oficial de Philipp Ludwig von Seidel (1821-1896) în 1874, de unde și numele ambilor matematicieni..
Pentru o înțelegere completă a metodei, este necesar să știm că o matrice este dominantă în diagonală atunci când valoarea absolută a elementului diagonal al fiecărui rând este mai mare sau egală cu suma valorilor absolute ale celorlalte elemente din același rând..
Matematic se exprimă astfel:
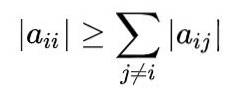
Indice articol
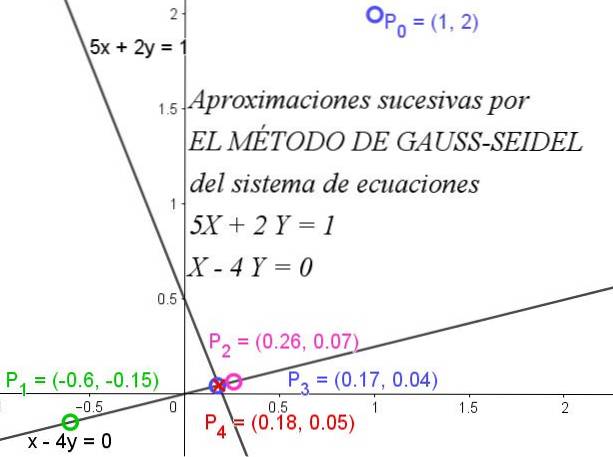
Pentru a ilustra în ce constă metoda Gauss-Seidel, vom lua un caz simplu, în care valorile lui X și Y pot fi găsite în sistemul de ecuații liniare 2 × 2 prezentat mai jos:
5X + 2Y = 1
X - 4Y = 0
1- În primul rând, este necesar să se determine dacă convergența este sigură. Se observă imediat că, de fapt, este un sistem dominant în diagonală, deoarece în primul rând primul coeficient are o valoare absolută mai mare decât celelalte din primul rând:
| 5 |> | 2 |
De asemenea, al doilea coeficient din al doilea rând este, de asemenea, dominant în diagonală:
| -4 |> | 1 |
Două- Variabilele X și Y sunt rezolvate:
X = (1 - 2Y) / 5
Y = X / 4
3- Se plasează o valoare inițială arbitrară, numită „sămânță”: Xo = 1, I = 2.
4-Începe iterația: pentru a obține prima aproximare X1, Y1, sămânța este substituită în prima ecuație a pasului 2 și rezultatul în a doua ecuație a pasului 2:
X1 = (1 - 2 I) / 5 = (1 - 2 × 2) / 5 = -3/5
Y1 = X1 / 4 = (-3/5) / 4 = -3/20
5- Procedăm în mod similar pentru a obține a doua aproximare a soluției sistemului de ecuații:
X2 = (1 - 2 Y1) / 5 = (1 - 2x (-3/20)) / 5 = 13/50
Y2 = X2 / 4 = (13/50) / 4 = 13/200
6- A treia iterație:
X3 = (1-2 Y2) / 5 = (1-2 (13/200)) / 5 = 87/500
Y3 = X3 / 4 = (87/500) / 4 = 87/2000
7- A patra iterație, ca iterație finală a acestui caz ilustrativ:
X4 = (1-2 Y3) / 5 = (1-2 (87/2000)) / 5 = 913/5000
Y4 = X4 / 4 = (913/5000) / 4 = 913/20000
Aceste valori sunt destul de bine de acord cu soluția găsită de alte metode de rezoluție. Cititorul îl poate verifica rapid cu ajutorul unui program matematic online.
După cum se poate observa, în metoda Gauss-Seidel, valorile aproximative obținute pentru variabila anterioară în aceeași etapă trebuie înlocuite în următoarea variabilă. Acest lucru îl diferențiază de alte metode iterative, cum ar fi cea a lui Jacobi, în care fiecare pas necesită aproximări ale etapei anterioare..
Metoda Gauss-Seidel nu este o procedură paralelă, în timp ce metoda Gauss-Jordan este. Este, de asemenea, motivul pentru care metoda Gauss-Seidel are o convergență mai rapidă - în mai puțini pași - decât metoda Jordan..
În ceea ce privește condiția matricei în diagonală, aceasta nu este întotdeauna satisfăcută. Cu toate acestea, în majoritatea cazurilor, simpla schimbare a rândurilor din sistemul original este suficientă pentru îndeplinirea condiției. Mai mult, metoda converge aproape întotdeauna, chiar și atunci când condiția de dominanță diagonală nu este îndeplinită..
Rezultatul anterior, obținut prin patru iterații ale metodei Gauss-Seidel, poate fi scris în formă zecimală:
X4 = 0,1826
Y4 = 0,04565
Soluția exactă la sistemul de ecuații propus este:
X = 2/11 = 0,1818
Y = 1/22 = 0,04545.
Deci, cu doar 4 iterații, veți obține un rezultat cu o miime de precizie (0,001).
Figura 1 ilustrează modul în care iterațiile succesive converg rapid către soluția exactă.
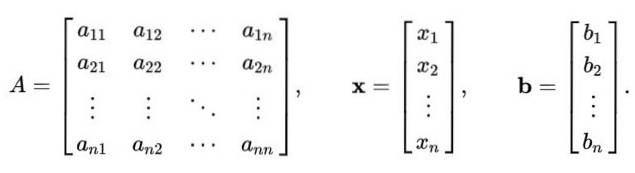
Metoda Gauss-Seidel nu este limitată doar la un sistem 2 × 2 de ecuații liniare. Procedura de mai sus poate fi generalizată pentru a rezolva un sistem liniar de n ecuații cu n necunoscute, care este reprezentată într-o matrice ca aceasta:
LA X = b
Unde LA este o matrice n x n, In timp ce X este vectorul n componente ale n variabile care urmează să fie calculate; Da b este un vector care conține valorile termenilor independenți.
Pentru a generaliza secvența de iterații aplicate în cazul ilustrativ unui sistem n x n, din care se calculează variabila Xi, se va aplica următoarea formulă:
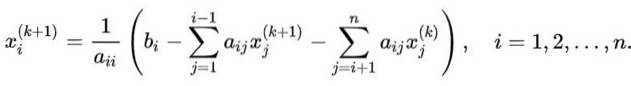
În această ecuație:
- k este indicele pentru valoarea obținută în iterație k.
-k + 1 indică noua valoare în cele ce urmează.
Numărul final de iterații este determinat atunci când valoarea obținută în iterație k + 1 diferă de cea obținută imediat înainte, printr-o cantitate ε care este exact precizia dorită.
Scrieți un algoritm general pentru a calcula vectorul soluțiilor aproximative X a unui sistem liniar de ecuații nxn, dată fiind matricea coeficienților LA, vectorul termenilor independenți b, numărul de iterații (iter) și valoarea inițială sau „seed” a vectorului X.
Algoritmul constă din două cicluri „Către”, unul pentru numărul de iterații și celălalt pentru numărul de variabile. Ar fi după cum urmează:
Pentru k ∊ [1 ... iter]
Pentru i ∊ [1 ... n]
X [i]: = (1 / A [i, i]) * (b [i] - ∑j = 1n(A [i, j] * X [j]) + A [i, i] * X [i])
Verificați funcționarea algoritmului anterior aplicându-l în software matematic SMath Studio gratuit de utilizat, disponibil pentru Windows și Android. Luați ca exemplu cazul matricei 2 × 2 care ne-a ajutat să ilustrăm metoda Gauss-Seidel.
Aplicați algoritmul Gauss-Seidel pentru următorul sistem de ecuații 3 × 3, care a fost anterior ordonat în așa fel încât coeficienții diagonalei să fie dominanți (adică de o valoare absolută mai mare decât valorile absolute ale coeficienților din același rând):
9 X1 + 2 X2 - X3 = -2
7 X1 + 8 X2 + 5 X3 = 3
3 X1 + 4 X2 - 10 X3 = 6
Utilizați vectorul nul ca semință și luați în considerare cinci iterații. Comentează rezultatul.
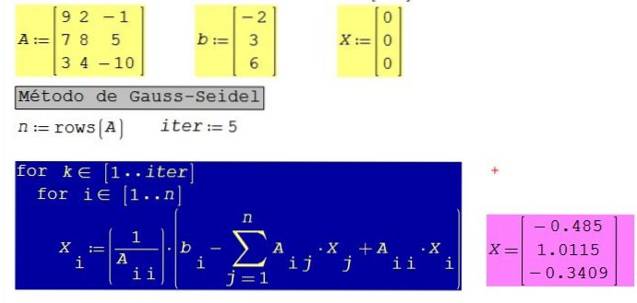
Pentru același sistem cu 10 iterații în loc de 5, se obțin următoarele rezultate: X1 = -0.485; X2 = 1,0123; X3 = -0,3406
Acest lucru ne spune că cinci iterații sunt suficiente pentru a obține trei zecimale de precizie și că metoda converge rapid către soluție.
Folosind algoritmul Gauss-Seidel dat mai sus, găsiți soluția la sistemul de ecuații 4 × 4 dat mai jos:
10 x1 - x2 + 2 x3 + 0 x4 = 6
-1 x1 + 11 x2 - 1 x3 + 3 x4 = 25
2 x1 - 1 x2 + 10 x3 - 1 x4 = -11
0 x1 + 3 x2 - 1 x3 + 8 x4 = 15
Pentru a începe metoda, utilizați această sămânță:
x1 = 0, x2 = 0, x3 = 0 și x4 = 0
Luați în considerare 10 iterații și estimați eroarea rezultatului, comparând cu numărul de iterație 11.
Atunci când se compară cu următoarea iterație (numărul 11), rezultatul este identic. Cele mai mari diferențe dintre cele două iterații sunt de ordinul 2 × 10-8, ceea ce înseamnă că soluția prezentată are o precizie de cel puțin șapte zecimale.
Nimeni nu a comentat acest articol încă.