
Conjugați exemple, exerciții de unghiuri interne și externe
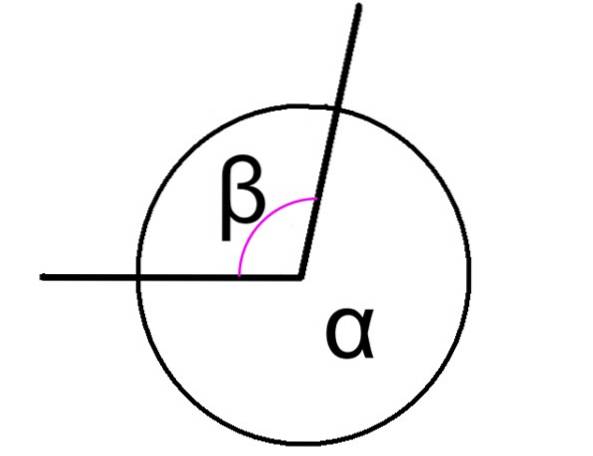
unghiuri conjugate Acestea sunt cele care, atunci când sunt adăugate, dau 360 ° ca rezultat, indiferent dacă aceste unghiuri sunt adiacente sau nu. În figura 1 sunt prezentate două unghiuri conjugate, notate ca α și β.
În acest caz, unghiurile α și β din figură au un vârf comun și laturile lor sunt comune, prin urmare sunt adiacente. Relația dintre ei este exprimată după cum urmează:
α + β = 360º
Pe de altă parte, să considerăm acum două linii paralele tăiate de o secantă, a căror dispunere este prezentată mai jos:
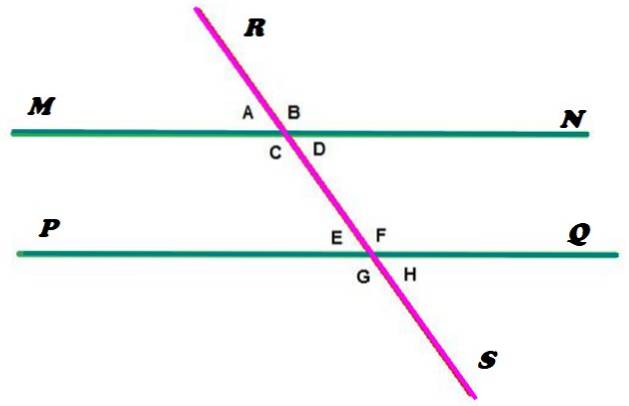
Liniile MN și PQ sunt paralele, în timp ce linia RS este secantă, intersectând paralelele în două puncte. După cum se poate vedea, această configurație determină formarea a 8 unghiuri, care au fost notate cu litere mici.
Ei bine, conform definiției date la început, unghiurile a, b, c și d sunt conjugate. Și în același mod e, f, g și h sunt, deoarece ambele cazuri sunt adevărate:
a + b + c + d = 360º
Da
e + f + g + h = 360º
Pentru această configurație, două unghiuri sunt conjugate dacă sunt pe aceeași parte în raport cu linia secantă RS și ambele sunt interne sau externe. În primul caz vorbim de unghiuri conjugate interne, în timp ce în al doilea, acestea sunt unghiuri conjugate externe.
Indice articol
- 1 Exemple
- 2 Unghiuri interne ale unui patrulater
- 2.1 Exemple
- 3 Exerciții
- 3.1 - Exercițiul 1
- 3.2 - Exercițiul 2
- 4 Referințe
Exemple
În figura 2, unghiurile externe sunt cele care se află în afara regiunii delimitate de liniile MN și PQ, acestea sunt unghiurile A, B, G și H. În timp ce unghiurile care se află între cele două linii sunt C, D, E și F.
Acum este necesar să analizăm ce unghiuri sunt la stânga și care la dreapta secantei.
În stânga RS sunt unghiurile A, C, E și G. Și în dreapta sunt unghiurile B, D, F și H.
Trecem imediat la determinarea perechilor de unghiuri conjugate, conform definiției date în secțiunea anterioară:
-A și G, externe și în stânga RS.
-D și F, interne și în dreapta RS.
-B și H, extern și în dreapta RS.
-C și E, intern și în stânga RS.
Proprietatea unghiurilor conjugate între linii paralele
Unghiurile conjugate dintre liniile paralele sunt suplimentare, adică suma lor este egală cu 180º. În acest fel, pentru figura 2 este adevărat următorul:
A + G = 180º
D + F = 180º
B + H = 180º
C + E = 180º
Perechile de unghiuri corespunzătoare pentru linii paralele
Acestea sunt cele care se află pe aceeași parte a liniei secante, nu sunt adiacente și una dintre ele este internă, iar cealaltă este externă. Este important să le vizualizați, deoarece măsura lor este aceeași, deoarece sunt unghiuri opuse de vârf.
Revenind la Figura 2, perechile de unghiuri corespunzătoare sunt identificate ca:
-A și E
-C și G
-B și F
-D și H
Unghiurile interne ale unui patrulater
Cadrilaterale sunt poligoane pe 4 laturi, printre care pătratul, dreptunghiul, trapezul, paralelogramul și rombul, de exemplu. Indiferent de forma lor, în oricare dintre ele este adevărat că suma unghiurilor lor interne este de 360 °, prin urmare îndeplinesc definiția dată la început..
Să vedem câteva exemple de patrulatere și cum să calculăm valoarea unghiurilor lor interne conform informațiilor din secțiunile precedente:
Exemple
a) Trei dintre unghiurile unui patrulater măsoară 75º, 110º și 70º. Cât ar trebui să măsoare unghiul rămas?
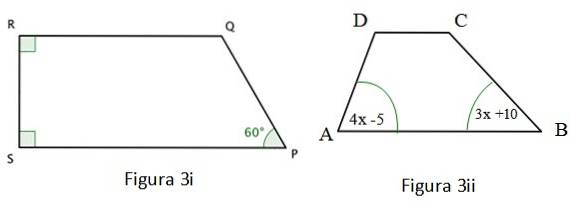
b) Găsiți valoarea unghiului ∠Q din figura 3 i.
c) Calculați măsura unghiului ∠A din figura 3 ii.
Solutie la
Fie α unghiul lipsă, este satisfăcut că:
α + 75º + 110º + 70º = 360º → α = 105º
Soluția b
Figura 3i prezentată este a trapezoidal și două dintre unghiurile sale interne sunt drepte, care au fost marcate cu un pătrat colorat la colțuri. Pentru acest patrulater se verifică următoarele:
∠R + ∠S + ∠P + ∠Q = 360º; ∠S = ∠R = 90 °; ∠P = 60º
Prin urmare:
∠ Q = 2 x 90º + 60º = 240º
Soluția c
Patrulaterul din figura 3 ii este, de asemenea, un trapez, pentru care sunt adevărate următoarele:
∠A + ∠B + ∠C + ∠D = 360º
Prin urmare:
4x -5 + 3x + 10 +180 = 360
7x + 5 = 180
x = (180 - 5) / 7
x = 25
Pentru a determina unghiul solicitat în enunț, folosim că ∠A = 4x - 5. Înlocuind valoarea calculată anterior a lui x rezultă că ∠A = (4 × 25) -5 = 95º
Instruire
- Exercitiul 1
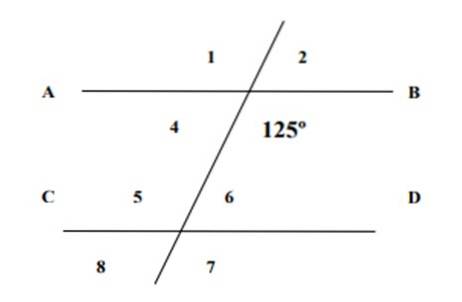
Știind că unul dintre unghiurile prezentate este de 125º, găsiți măsurile celor 7 unghiuri rămase în figura următoare și justificați răspunsurile.
Soluţie
Unghiul 6 și unghiul 125º sunt conjugate interne, a căror sumă este 180º, conform proprietății unghiurilor conjugate, prin urmare:
∠6 + 125º = 180º → ∠6 = 180º - 125º = 55º
Pe de altă parte, ∠6 și ∠8 sunt unghiuri opuse de vârf, a căror măsură este aceeași. Prin urmare, ∠8 măsoară 55º.
Unghiul ∠1 este, de asemenea, opus de vârf la 125º, atunci putem afirma că ∠1 = 125º. De asemenea, putem apela la faptul că perechile de unghiuri corespunzătoare au aceeași măsură. În figură, aceste unghiuri sunt:
∠7 = 125 º
∠2 = ∠6 = 55 º
∠1 = ∠5 = 125º
∠4 = ∠8 = 55 º
- Exercițiul 2
Găsiți valoarea lui x în figura următoare și valorile tuturor unghiurilor:
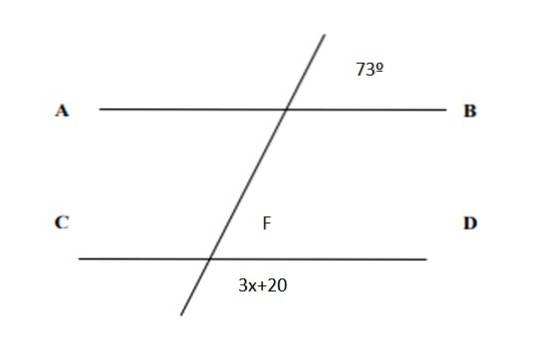
Soluţie
Deoarece sunt perechi corespunzătoare, rezultă că F = 73º. Și, pe de altă parte, suma perechilor conjugate este de 180 °, deci:
3x + 20º + 73º = 180º
3x = 180º - 73º -20º = 87
În cele din urmă, valoarea lui x este:
x = 87/3 = 29
În ceea ce privește toate unghiurile, acestea sunt enumerate în figura următoare:
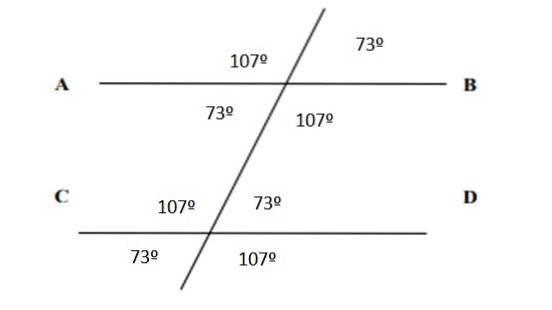
Referințe
- Grupuri unghiulare. Explicații privind unghiurile complementare, suplimentare și explicative. Recuperat de pe: thisiget.com/
- Baldor, A. 1983. Geometrie și trigonometrie plană și spațială. Grupul Cultural Patria.
- Corral, M. Matematica LibreTexte: Unghiuri. Recuperat de pe: math.libretexts.org.
- Mathmania. Clasificarea și construirea unghiurilor după măsurarea lor. Recuperat de pe: mathemania.com/
- Wentworth, G. Plane Geometry. Recuperat de pe: gutenberg.org.
- Wikipedia. Conjugați unghiuri. Recuperat de pe: es.wikipedia.org.



Nimeni nu a comentat acest articol încă.