
Proprietăți de numere imaginare, aplicații, exemple
numere imaginare sunt cele care dau o soluție ecuației în care necunoscutul, pătrat, este egal cu un număr real negativ. Unitatea imaginară este i = √ (-1).
În ecuație: zDouă= - a, z este un număr imaginar care se exprimă după cum urmează:
z = √ (-a) = i√ (a)
Fiind la un număr real pozitiv. da a = 1, atunci z = i, Unde eu este unitatea imaginară.
În general, un număr imaginar pur z este întotdeauna exprimat sub forma:
z = y⋅i
Unde Da este un număr real e eu este unitatea imaginară.
La fel ca numerele reale sunt reprezentate pe o linie, numită adevărat drept, într-un mod analog numerele imaginare sunt reprezentate pe linie imaginară.
linie imaginară este întotdeauna ortogonală (formă de 90º) față de adevărat drept iar cele două linii definesc un plan cartezian numit plan complex.
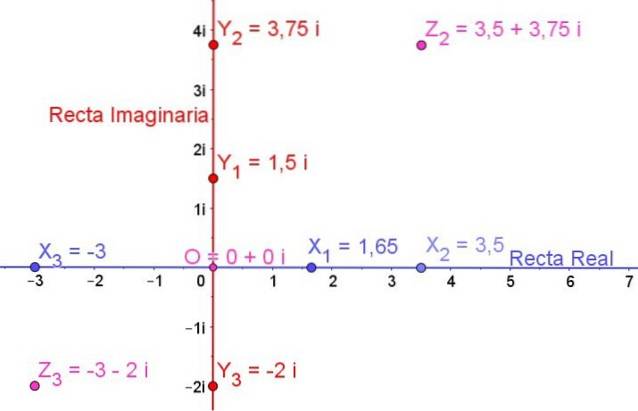
În figura 1 este prezentat planul complex și pe el sunt reprezentate unele numere reale, unele numere imaginare și, de asemenea, unele numere complexe:
X1, XDouă, X3 sunt numere reale
Da1, DaDouă, Da3 sunt numere imaginare
ZDouă și Z3 sunt numere complexe
Numărul O este zero real și este și zero imaginar, deci originea O este zero complex exprimat prin:
0 + 0i
Indice articol
- 1 Proprietăți
- 1.1 Adunarea și scăderea imaginarului
- 1.2 Produsul imaginarilor
- 1.3 Produsul unui număr real de către un alt imaginar
- 1.4 Împuternicirea unui imaginar
- 1.5 Suma unui număr real și a unui număr imaginar
- 2 Aplicații
- 3 Exerciții cu numere imaginare
- 3.1 - Exercițiul 1
- 3.2 - Exercițiul 2
- 3.3 - Exercițiul 3
- 3.4 - Exercițiul 4
- 3.5 - Exercițiul 5
- 3.6 - Exercițiul 6
- 4 Referințe
Proprietăți
Setul de numere imaginare este notat prin:
I = …, -3i,…, -2i,…., - i,…., 0i,…., I,…., 2i,…., 3i,…
Și puteți defini câteva operații pe acest set numeric. Un număr imaginar nu este întotdeauna obținut din aceste operații, așa că să le privim mai puțin detaliat:
Adunarea și scăderea imaginarului
Numerele imaginare pot fi adăugate și scăzute unele de altele, rezultând un nou număr imaginar. De exemplu:
3i + 2i = 5i
4i - 7i = -3i
Produs al imaginarului
Când se realizează produsul unui număr imaginar cu altul, rezultatul este un număr real. Să facem următoarea operație pentru a o verifica:
2i x 3i = 6 x iDouă = 6 x (√ (-1))Două = 6 x (-1) = -6.
Și, după cum putem vedea, -6 este un număr real, deși a fost obținut prin înmulțirea a două numere imaginare pure.
Produs al unui număr real de către un alt imaginar
Dacă un număr real este înmulțit cu i, rezultatul va fi un număr imaginar, care corespunde unei rotații de 90 de grade în sens invers acelor de ceasornic.
Și este că iDouă corespunde la două rotații consecutive de 90 de grade, ceea ce echivalează cu înmulțirea cu -1, adică iDouă = -1. Poate fi văzut în următoarea diagramă:
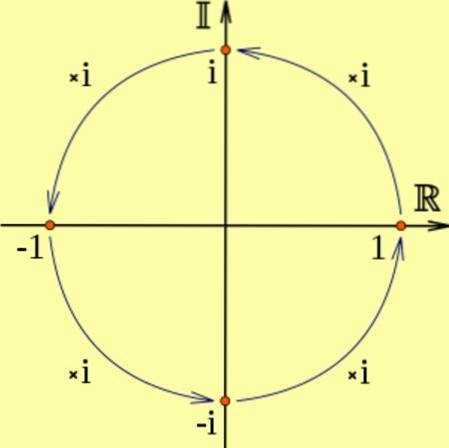
De exemplu:
-3 x 5i = -15i
-3 x i = -3i.
Împuternicirea unui imaginar
Puteți defini potențarea unui număr imaginar la un exponent întreg:
eu1 = i
euDouă = i x i = √ (-1) x √ (-1) = -1
eu3 = i x iDouă = -i
eu4 = iDouă x iDouă = -1 x -1 = 1
eu5 = i x i4 = i
În general trebuie eun = i ^ (n mod 4), Unde mod este restul diviziunii dintre n Da 4.
Potențierea negativă a numărului întreg poate fi efectuată și:
eu-1 = 1 / i1 = i / (i x i1) = i / (iDouă) = i / (-1) = -i
eu-Două = 1 / iDouă = 1 / (-1) = -1
eu-3= 1 / i3 = 1 / (- i) = (-1) / i = -1 x i-1 = (-1) x (-i) = i
În general, numărul imaginar b⋅i ridicat la puterea n este:
(b⋅i) in = bn eun = bn i ^ (n mod 4)
Câteva exemple sunt următoarele:
(5 i)12 = 512 eu12 = 512 eu0 = 512 x 1 = 244140625
(5 i)unsprezece = 5unsprezece euunsprezece = 5unsprezece eu3 = 5unsprezece x (-i) = -48828125 i
(-2 i)10 = -210 eu10 = 210 euDouă = 1024 x (-1) = -1024
Suma unui număr real și a unui număr imaginar
Când adăugați un număr real cu unul imaginar, rezultatul nu este nici real, nici imaginar, este un nou tip de număr numit număr complex.
De exemplu, dacă X = 3,5 și Y = 3,75i, atunci rezultatul este numărul complex:
Z = X + Y = 3,5 + 3,75 i
Rețineți că în sumă părțile reale și imaginare nu pot fi grupate împreună, deci un număr complex va avea întotdeauna o parte reală și o parte imaginară..
Această operație extinde setul de numere reale la cel mai larg dintre numere complexe.
Aplicații
Numele numerelor imaginare a fost propus de matematicianul francez René Descartes (1596-1650) ca o batjocură sau dezacord cu propunerea aceluiași făcută de matematicianul italian al secolului Raffaelle Bombelli.
Alți mari matematicieni, precum Euler și Leibniz, l-au susținut pe Descartes în acest dezacord și au numit numere imaginare numere de amfibieni, care erau rupte între ființă și nimic.
Numele numerelor imaginare rămâne astăzi, dar existența și importanța lor sunt foarte reale și palpabile, deoarece apar în mod natural în multe domenii ale fizicii, cum ar fi:
-Teoria relativității.
-În electromagnetism.
-Mecanica cuantică.
Exerciții cu numere imaginare
- Exercitiul 1
Găsiți soluțiile următoarei ecuații:
zDouă + 16 = 0
Soluţie
zDouă = -16
Având rădăcină pătrată în ambii membri avem:
√ (zDouă ) = √ (-16)
± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i
Cu alte cuvinte, soluțiile ecuației originale sunt:
z = + 4i sau z = -4i.
- Exercițiul 2
Găsiți rezultatul ridicării unității imaginare la puterea 5 minus scăderea unității imaginare ridicată la puterea -5.
Soluţie
eu5 - eu-5 = i5 - 1 / i5 = i - 1 / i = i - (i) / (i x i) = i - i / (- 1) = i + i = 2i
- Exercițiul 3
Găsiți rezultatul următoarei operații:
(3i)3 + 9i
Soluţie
33 eu3 - 9 = 9 (-i) + 9i = -9i + 9i = 0i
- Exercițiul 4
Găsiți soluțiile următoarei ecuații pătratice:
(-2x)Două + 2 = 0
Soluţie
Ecuația este rearanjată după cum urmează:
(-2x)Două = -2
Apoi se ia rădăcina pătrată a ambilor membri
√ ((- 2x)Două) = √ (-2)
± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i
Apoi rezolvăm pentru x pentru a obține în cele din urmă:
x = ± √2 / 2 i
Adică, există două soluții posibile:
x = (√2 / 2) i
Sau celălalt:
x = - (√2 / 2) i
- Exercițiul 5
Găsiți valoarea lui Z definită de:
Z = √ (-9) √ (-4) + 7
Soluţie
Știm că rădăcina pătrată a unui număr real negativ este un număr imaginar, de exemplu √ (-9) este egal cu √ (9) x √ (-1) = 3i.
Pe de altă parte, √ (-4) este egal cu √ (4) x √ (-1) = 2i.
Deci ecuația originală poate fi înlocuită cu:
3i x 2i - 7 = 6 iDouă - 7 = 6 (-1) - 7 = -6 - 7 = -13
- Exercițiul 6
Găsiți valoarea lui Z rezultată din următoarea împărțire a două numere complexe:
Z = (9 - iDouă) / (3 + i)
Soluţie
Numeratorul expresiei poate fi luat în calcul folosind următoarea proprietate:
O diferență de pătrate este produsul sumei și diferenței binomilor fără pătrat.
Atunci:
Z = [(3 - i) (3 + i)] / (3 + i)
Expresia rezultată este apoi simplificată, părăsind
Z = (3 - i)
Referințe
- Earl, R. Numere complexe. Recuperat de la: maths.ox.ac.uk.
- Figuera, J. 2000. Matematica 1. Diversificat. Ediții CO-BO.
- Hoffmann, J. 2005. Selecția subiectelor de matematică. Publicații Monfort.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Wikipedia. Număr imaginar. Recuperat de pe: en.wikipedia.org



Nimeni nu a comentat acest articol încă.