
Papomudas Cum să le rezolvați și exerciții
papomudas este o procedură de rezolvare a expresiilor algebrice. Acronimele sale indică ordinea de prioritate a operațiilor: paranteze, puteri, multiplicare, divizare, adunare și scădere. Folosind acest cuvânt vă puteți aminti cu ușurință ordinea în care trebuie să rezolvați o expresie compusă din mai multe operații.
În general, în expresiile numerice, mai multe operații aritmetice pot fi găsite împreună, cum ar fi adunarea, scăderea, înmulțirea și divizarea, care pot fi și fracții, puteri și rădăcini. Pentru a le rezolva, este necesar să urmați o procedură care garantează că rezultatele vor fi corecte..

O expresie aritmetică care este alcătuită dintr-o combinație a acestor operații trebuie rezolvată în funcție de prioritatea ordinii, cunoscută și sub numele de ierarhia operațiilor, stabilită de mult în convențiile universale. Astfel, toți oamenii pot urma aceeași procedură și pot obține același rezultat.
Indice articol
- 1 Caracteristici
- 2 Cum să le rezolvi?
- 3 Cerere
- 3.1 Expresii care conțin adunare și scădere
- 3.2 Expresii care conțin adunare, scădere și multiplicare
- 3.3 Expresii care conțin adunare, scădere, multiplicare și divizare
- 3.4 Expresii care conțin adunare, scădere, multiplicare, împărțire și puteri
- 3.5 Expresii care utilizează simboluri de grupare
- 4 Exerciții
- 4.1 Primul exercițiu
- 4.2 Al doilea exercițiu
- 4.3 Al treilea exercițiu
- 5 Referințe
Caracteristici
Papomudas este o procedură standard care stabilește ordinea care trebuie urmată la rezolvarea unei expresii, care este compusă dintr-o combinație de operații precum adunarea, scăderea, înmulțirea și împărțirea..
Cu această procedură, ordinea de prioritate a unei operații este stabilită în raport cu celelalte în momentul în care vor fi rezultate; adică fiecare operațiune are o schimbare sau un nivel ierarhic de rezolvat.
Ordinea în care trebuie rezolvate diferitele operații ale unei expresii este dată de fiecare acronim al cuvântului papomudas. Astfel, trebuie să:
1- Pa: paranteze, paranteze sau paranteze.
2- Po: puteri și rădăcini.
3- Mu: multiplicări.
4- D: diviziuni.
5- A: adăugiri sau adăugiri.
6- S: scăderi sau scăderi.
Această procedură este, de asemenea, numită în limba engleză sub numele de PEMDAS; să ne amintim cu ușurință acest cuvânt este asociat cu expresia: "Pcitit ȘIxcuse MDa Dureche LAunt Saliat”, Unde fiecare literă inițială corespunde unei operații aritmetice, în același mod ca papomudas.
Cum să le rezolvi?
Pe baza ierarhiei stabilite de papomudas pentru a rezolva operațiunile unei expresii, este necesar să se îndeplinească următoarea ordine:
- Toate operațiunile din cadrul grupării simbolurilor, cum ar fi paranteze, paranteze, paranteze pătrate și bare de fracție, trebuie mai întâi rezolvate. Când există gruparea simbolurilor în interiorul altora, trebuie să începeți să calculați din interior spre exterior.
Aceste simboluri sunt folosite pentru a schimba ordinea în care sunt rezolvate operațiile, deoarece ceea ce este în interiorul lor trebuie întotdeauna rezolvat mai întâi..
- Apoi, puterile și rădăcinile sunt rezolvate.
- În al treilea rând, se rezolvă multiplicările și diviziunile. Acestea au aceeași ordine de prioritate; prin urmare, atunci când aceste două operații se găsesc într-o expresie, cea care apare mai întâi trebuie rezolvată, citind expresia de la stânga la dreapta.
- În ultimul rând, sunt rezolvate adunările și scăderile, care au, de asemenea, aceeași ordine de prioritate și, prin urmare, cea care apare prima în expresie, citită de la stânga la dreapta, este rezolvată.
- Operațiunile nu trebuie amestecate niciodată atunci când sunt citite de la stânga la dreapta, ordinea de prioritate sau ierarhie stabilită de papomuda trebuie întotdeauna respectată..
Este important să ne amintim că rezultatul fiecărei operații trebuie să fie plasat în aceeași ordine în raport cu celelalte și că toți pașii intermediari trebuie separați printr-un semn până când se ajunge la rezultatul final..
Aplicație
Procedura papomudas este utilizată atunci când aveți o combinație de operații diferite. Ținând cont de modul în care sunt rezolvate, acest lucru poate fi aplicat în:
Expresii care conțin adunare și scădere
Este una dintre cele mai simple operații, deoarece ambele au aceeași ordine de prioritate, în așa fel încât trebuie rezolvată începând de la stânga la dreapta în expresie; de exemplu:
22 -15 + 8 +6 = 21.
Expresii care conțin adunare, scădere și multiplicare
În acest caz, operația cu cea mai mare prioritate este multiplicarea, apoi adunarea și scăderea sunt rezolvate (oricare dintre acestea este prima din expresie). De exemplu:
6 * 4 - 10 + 8 * 6 - 16 + 10 * 6
= 24 -10 + 48 - 16 + 60
= 106.
Expresii care conțin adunare, scădere, multiplicare și divizare
În acest caz aveți o combinație a tuturor operațiunilor. Începeți prin rezolvarea multiplicării și divizării care au prioritate mai mare, apoi adunarea și scăderea. Citind expresia de la stânga la dreapta, aceasta este rezolvată în funcție de ierarhia și poziția sa în cadrul expresiei; de exemplu:
7 + 10 * 13 - 8 + 40 ÷ 2
= 7 + 130 - 8 + 20
= 149.
Expresii care conțin adunare, scădere, multiplicare, împărțire și puteri
În acest caz, unul dintre numere este ridicat la o putere, care în cadrul nivelului de prioritate trebuie rezolvată mai întâi, pentru a rezolva apoi înmulțirile și împărțirile și, în final, adunările și scăderile:
4 + 4Două * 12 - 5 + 90 ÷ 3
= 4 + 16 * 12 - 5 + 90 ÷ 3
= 4 + 192 - 5 + 30
= 221.
La fel ca puterile, rădăcinile au și a doua ordine de prioritate; Prin urmare, în expresiile care le conțin, multiplicarea, împărțirea, adunarea și scăderea trebuie rezolvate mai întâi:
5 * 8 + 20 ÷ √16
= 5 * 8 + 20 ÷ 4
= 40 + 5
= 45.
Expresii care utilizează simboluri de grupare
Când sunt folosite semne precum paranteze, paranteze, paranteze și bare de fracțiune, ceea ce este în interiorul acestora este rezolvat mai întâi, indiferent de ordinea de prioritate a operațiilor pe care le conține în raport cu cele din afara acesteia, ca și cum ar fi o expresie separată :
14 ÷ 2 - (8 - 5)
= 14 ÷ 2 - 3
= 7 - 3
= 4.
Dacă există mai multe operațiuni în cadrul acestuia, acestea trebuie rezolvate în ordine ierarhică. Apoi celelalte operații care alcătuiesc expresia sunt rezolvate; de exemplu:
2 + 9 * (5 + 23 - 24 ÷ 6) - 1
= 2 + 9 * (5 + 8 - 4) - 1
= 2 + 9 * 9 - 1
= 2 + 81 - 1
= 82.
Unele expresii folosesc gruparea simbolurilor în altele, cum ar fi atunci când este necesar să se schimbe semnul unei operații. În aceste cazuri, trebuie să începeți prin rezolvarea din interior spre exterior; adică simplificarea simbolurilor de grupare care se află în centrul unei expresii.
În general, ordinea de rezolvare a operațiilor conținute în cadrul acestor simboluri este: mai întâi rezolvați ceea ce se află în paranteze (), apoi paranteze [] și ultima paranteze .
90 - 3*[12 + (5*4) - (4*Două)]
= 90 - 3* [12 + 20 - 8]
= 90 - 3 * 24
= 90 - 72
= 18.
Instruire
Primul exercițiu
Găsiți valoarea următoarei expresii:
douăzeciDouă + √225 - 155 + 130.
Soluţie
Aplicând papomudas, puterile și rădăcinile trebuie rezolvate mai întâi, apoi adunarea și scăderea. În acest caz, primele două operații aparțin aceleiași ordine, deci cea care este prima este rezolvată, începând de la stânga la dreapta:
douăzeciDouă + √225 - 155 + 130
= 400 + 15 -155 + 130.
Apoi adăugați și scădeți, începând și din stânga:
400 + 15 -155 + 130
= 390.
Al doilea exercițiu
Găsiți valoarea următoarei expresii:
[- (63 - 36) ÷ (8 * 6 ÷ 16)].
Soluţie
Începe prin rezolvarea operațiilor care se află în interiorul parantezelor, urmând ordinea ierarhică pe care o au conform papomudas.
Mai întâi sunt rezolvate puterile primei paranteze, apoi sunt rezolvate operațiile celei de-a doua paranteze. Deoarece aparțin aceleiași ordine, prima operație a expresiei este rezolvată:
[- (63 - 36) ÷ (8 * 6 ÷ 16)]
= [- (216 - 729) ÷ (8 * 6 ÷ 16)]
= [- (216 - 729) ÷ (48 ÷ 16)]
= [- (-513) ÷ (3)].
Deoarece operațiunile din paranteze au fost deja rezolvate, acum continuăm cu diviziunea care are o ierarhie mai mare decât scăderea:
[- (-513) ÷ (3)] = [- (-171)].
În cele din urmă, parantezele care separă semnul minus (-) de rezultat, care în acest caz este negativ, indică faptul că aceste semne trebuie multiplicate. Astfel, rezultatul expresiei este:
[- (-171)] = 171.
Al treilea exercițiu
Găsiți valoarea următoarei expresii:

Soluţie
Începeți prin rezolvarea fracțiilor care se află în paranteze:
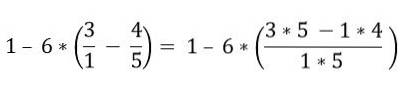
În interiorul parantezelor există mai multe operații. Înmulțirile sunt rezolvate mai întâi și apoi scăderile; În acest caz, bara de fracție este considerată ca un simbol de grupare și nu ca o divizare, din acest motiv operațiunile părții superioare și inferioare trebuie rezolvate:
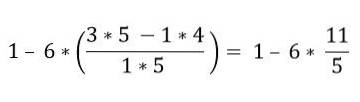
În ordine ierarhică, multiplicarea trebuie rezolvată:
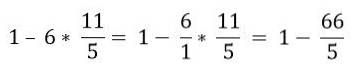
În cele din urmă, scăderea este rezolvată:
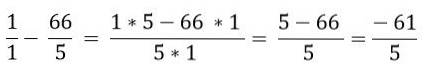
Referințe
- Aguirre, H. M. (2012). Matematica financiară. Cengage Learning.
- Aponte, G. (1998). Fundamentele matematicii de bază. Pearson Education.
- Cabanne, N. (2007). Didactica matematicii.
- Carolina Espinosa, C. C. (2012). Resurse în operațiile de învățare.
- Huffstetler, K. (2016). Povestea Ordinului Operațiunilor: Pemdas. Creați spațiu independent .
- Madore, B. (2009). Cartea de lucru GRE Math. Seria educațională a lui Barron,.
- Molina, F. A. (s.f.). Proiect Azarquiel, Matematică: Primul ciclu. Grupul Azarquiel.



Nimeni nu a comentat acest articol încă.