
Perimetrul cercului cum să-l scoți și formule, exerciții rezolvate

perimetru cerc este ansamblul de puncte care formează conturul unui cerc și este, de asemenea, cunoscut sub numele de lungime a circumferinței. Depinde de rază, deoarece o circumferință mai mare va avea, evident, un contur mai mare.
Fi P perimetrul unui cerc și R raza acestuia, atunci putem calcula P cu următoarea ecuație:
P = 2π.R

Unde π este un număr real (citiți „pi”) care valorează aproximativ 3,1416 ... Elipsa se datorează faptului că π are infinite zecimale. Prin urmare, atunci când faceți calcule, este necesar să se rotunjească valoarea acestuia.
Cu toate acestea, pentru majoritatea aplicațiilor, este suficient să luați suma indicată aici sau să utilizați toate zecimalele pe care le returnează calculatorul cu care lucrați..
Dacă în loc să aibă raza, este preferabil să se utilizeze diametrul D, care știm că este de două ori raza, perimetrul se exprimă după cum urmează:
P = π.2R = π.D
Deoarece perimetrul are o lungime, acesta trebuie să fie întotdeauna exprimat în unități precum metri, centimetri, picioare, inci și multe altele, în funcție de sistemul preferat..
Indice articol
- 1 Circumferințe și cercuri
- 2 Exerciții demonstrative pentru calcularea perimetrului cercului
- 2.1 - Exercițiul 1
- 2.2 - Exercițiul 2
- 2.3 - Exercițiul 3
- 3 Aplicații
- 4 Referințe
Circumferințe și cercuri
Acestea sunt adesea termeni care sunt folosiți în mod interschimbabil, adică sinonim. Dar se întâmplă să existe diferențe între ele.
Cuvântul „perimetru” provine din grecescul „peri” care înseamnă contur și „metru” sau măsură. Circumferința este conturul sau perimetrul cercului. În mod formal, acesta este definit după cum urmează:
Un cerc este ansamblul de puncte cu distanță egală cu un punct numit centru, această distanță fiind raza circumferinței.
La rândul său, cercul este definit după cum urmează:
Un cerc este ansamblul de puncte a căror distanță până la un punct numit centru este mai mic sau egal la o distanță fixă numită radio.
Cititorul poate vedea diferența subtilă dintre cele două concepte. Circumferința se referă doar la setul de puncte ale muchiei, în timp ce cercul este setul de puncte de la margine la interior, dintre care circumferința este marginea.
Exerciții ddemonstrație de calcul a perimetrului cercului
Prin exercițiile următoare, conceptele descrise mai sus vor fi puse în practică, precum și unele altele care vor fi explicate pe măsură ce apar. Vom începe de la cel mai simplu și gradul de dificultate va crește progresiv.
- Exercitiul 1
Găsiți perimetrul și aria cercului cu raza de 5 cm.
Soluţie
Ecuația dată la început se aplică direct:
P = 2π.R= 2π.5 cm = 10 π cm = 31,416 cm
Pentru a calcula aria LA se folosește următoarea formulă:
LA = π.RDouă = π. (5cm)Două= 25π cmDouă= 78,534 cmDouă
- Exercițiul 2
a) Găsiți perimetrul și aria regiunii goale în figura următoare. Centrul cercului umbrit se află în punctul roșu, în timp ce centrul cercului alb este punctul verde.
b) Repetați secțiunea anterioară pentru regiunea umbrită.
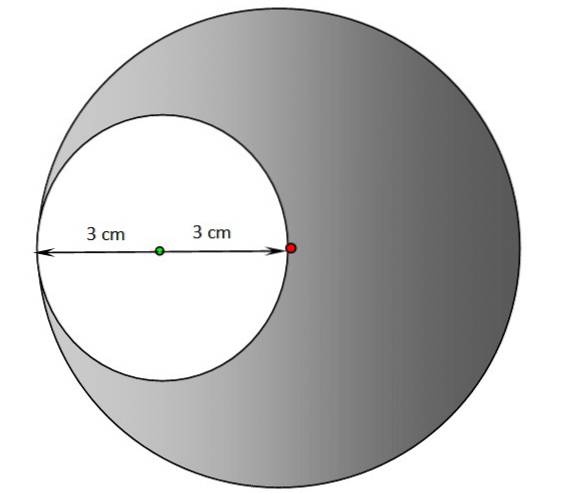
Soluţie
a) Raza cercului alb este de 3 cm, de aceea aplicăm aceleași ecuații ca în exercițiul 1:
P = 2π.R= 2π.3 cm = 6 π cm = 18,85 cm
LA = π.RDouă = π. (3cm)Două= 9π cmDouă= 28,27 cmDouă
b) Pentru cercul umbrit, raza este de 6 cm, perimetrul său este dublu față de cel calculat în secțiunea a):
P = 2π.R= 2π.6 cm = 12 π cm = 37,70 cm
Și, în cele din urmă, aria regiunii umbrite este calculată după cum urmează:
- Mai întâi găsim zona cercului umbrit ca și cum ar fi completă, pe care o vom numi A ', astfel:
LA' = π.RDouă= π. (6 cm)Două = 36π cmDouă= 113,10 cmDouă
- Apoi în zonă LA' Se scade aria cercului alb, calculată anterior în secțiunea a), astfel se obține aria solicitată, care va fi notată pur și simplu ca A:
A = A '- 28,27 cmDouă = 113.10-28.27 cmDouă = 84,83 cmDouă
- Exercițiul 3
Găsiți zona și perimetrul regiunii umbrite în următoarea figură:
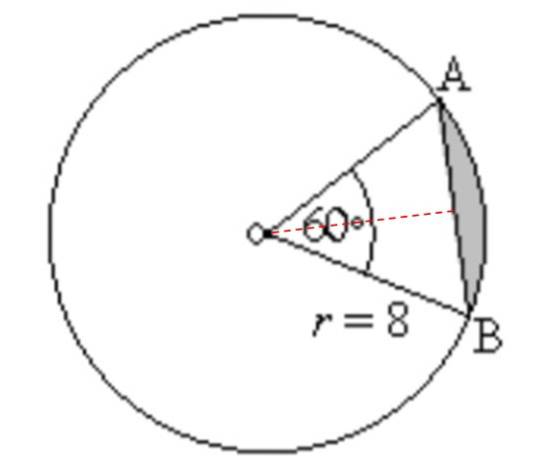
Soluţie
Calculul ariei regiunii umbrite
Calculăm mai întâi aria de sector circular sau pană, între segmentele drepte OA și OB și segmentul circular AB, așa cum se arată în figura următoare:
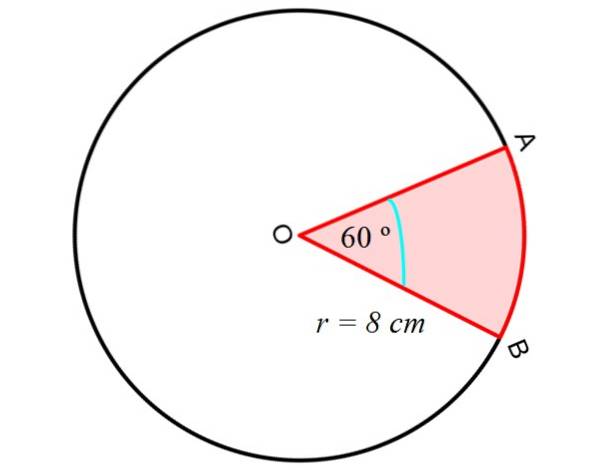
Pentru aceasta, se folosește următoarea ecuație, care ne oferă aria unui sector circular, cunoscând raza R și unghiul central dintre segmentele OA și OB, adică două dintre razele circumferinței:
LA sector circular = Π.RDouă. (αº / 360º)
Unde αº este unghiul central - este central deoarece vârful său este centrul circumferinței - între două raze.
Pasul 1: calculați aria sectorului circular
Astfel, aria sectorului prezentat în figură este:
LA sector circular = Π.RDouă. (αº / 360º) = π. (8 cm)Două. (60º / 360º) = (64/6) π cmDouă= 33,51 cmDouă
Pasul 2: calculați aria triunghiului
În continuare vom calcula aria triunghiului alb din figura 3. Acest triunghi este echilateral și aria sa este:
LA triunghi = (1/2) bază x înălțime
Înălțimea este linia punctată roșie văzută în figura 4. Pentru a o găsi, puteți utiliza teorema lui Pitagora, de exemplu. Dar nu este singura cale.
Cititorul atent va observa că triunghiul echilateral este împărțit în două triunghiuri dreptunghiulare identice, a căror bază este de 4 cm:
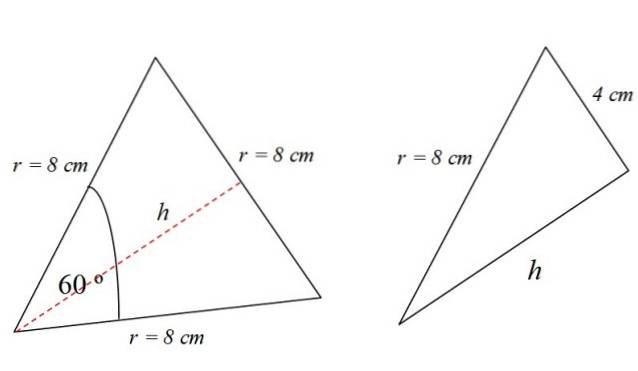
Într-un triunghi dreptunghiular, teorema lui Pitagora este îndeplinită, prin urmare:

LA triunghi = (1/2) bază x înălțime = (1/2) 8 cm x 6,93 cm = 27,71 cmDouă.
Pasul 3: calcularea zonei umbrite
Este suficient să scădeți aria mai mare (cea a sectorului circular) din zona mai mică (cea a triunghiului echilateral): A regiune umbrită = 33,51 cmDouă - 27,71 cmDouă = 5,80 cmDouă.
Calculul perimetrului regiunii umbrite
Perimetrul căutat este suma laturii rectilinii de 8 cm și a arcului de circumferință AB. Acum, circumferința completă subtinde 360º, prin urmare un arc care subtinde 60º este o șesime din lungimea completă, despre care știm că este 2.π.R
AB = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm
Înlocuind, perimetrul regiunii umbrite este:
P = 8 cm + 8,38 cm = 16,38 cm.
Aplicații
Perimetrul, ca și zona, este un concept foarte important în geometrie și cu multe aplicații în viața de zi cu zi..
Artiștii, designerii, arhitecții, inginerii și mulți alți oameni folosesc perimetrul în timp ce își dezvoltă munca, în special cea a unui cerc, deoarece forma rotundă este peste tot: de la publicitate, prin mâncare la mașini.

Pentru a cunoaște direct lungimea unei circumferințe, este suficient să o înfășurați cu un fir sau un șir, apoi să extindeți acest fir și să îl măsurați cu o bandă măsurătoare. Cealaltă alternativă este de a măsura raza sau diametrul cercului și de a utiliza una dintre formulele descrise mai sus..
În munca de zi cu zi, conceptul de perimetru este utilizat atunci când:
-Matrița potrivită este aleasă pentru o anumită dimensiune de pizza sau tort.
-Un drum urban va fi proiectat, calculând dimensiunea unui flacon în care mașinile se pot întoarce pentru a schimba direcția.
-Știm că Pământul se învârte în jurul Soarelui pe o orbită aproximativ circulară - orbitele planetare sunt de fapt eliptice, conform legilor lui Kepler - dar circumferința este o aproximare foarte bună pentru majoritatea planetelor..
-Dimensiunea adecvată a unui inel este aleasă pentru a fi cumpărată într-un magazin online.
-Alegem o cheie de dimensiunea potrivită pentru a slăbi o piuliță.
Si multe altele.
Referințe
- Tutoriale gratuite de matematică. Aria și perimetrul unui cerc - Calculator de geometrie. Recuperat de pe: analyzemath.com.
- Math Open Reference. Circumferință, perimetrul unui cerc. Recuperat de pe: mathopenref.com.
- Institutul Monterey. Perimetru și zonă. Recuperat de pe: montereyinstitute.org.
- Știința. Cum se găsește perimetrul unui cerc. Recuperat de pe: sciencing.com.
- Wikipedia. Circumferinţă. Recuperat de pe: en.wikipedia.org.


Nimeni nu a comentat acest articol încă.