probabilitatea teoretică (sau Laplace) că apare un eveniment E care aparține unui spațiu eșantion S, în care toate evenimentele au aceeași probabilitate de apariție, este definit în notație matematică ca: P (E) = n (E) / N (S)
Unde P (E) este probabilitatea, dată ca coeficientul dintre numărul total de rezultate posibile ale evenimentului E, pe care îl numim n (E), împărțit la numărul total N (S) de rezultate posibile în spațiul eșantion S.
Probabilitatea teoretică este un număr real între 0 și 1, dar este adesea exprimată ca procent, caz în care probabilitatea va fi o valoare între 0% și 100%.
Calculul probabilității producerii unui eveniment este foarte important în multe domenii, cum ar fi tranzacționarea, companiile de asigurări, jocurile de noroc și multe altele..
Indice articol
Un caz ilustrativ este cazul tombolelor sau loteriilor. Să presupunem că sunt emise 1.000 de bilete pentru tombola unui smartphone. Deoarece extragerea se face la întâmplare, oricare dintre bilete are șanse egale de a fi câștigător.
Pentru a găsi probabilitatea ca o persoană care cumpără un bilet cu numărul 81 să fie câștigătoare, următorul calcul al probabilitatea teoretică:
P (1) = 1 / 1.000 = 0,001 = 0,1%
Rezultatul anterior este interpretat după cum urmează: dacă extragerea ar fi repetată infinit de multe ori, la fiecare 1.000 de ori biletul 81 ar fi selectat, în medie, o dată.
Dacă din anumite motive cineva achiziționează toate biletele, este sigur că va câștiga premiul. Probabilitatea de a câștiga premiul dacă aveți toate biletele este calculată după cum urmează:
P (1.000) = 1.000 / 1.000 = 1 = 100%.
Adică, probabilitatea 1 sau 100% înseamnă că este total sigur că acest rezultat va apărea..
Dacă cineva deține 500 de bilete, șansele de a câștiga sau de a pierde sunt aceleași. Probabilitatea teoretică de a câștiga premiul în acest caz este calculată după cum urmează:
P (500) = 500 / 1.000 = ½ = 0,5 = 50%.
Cel care nu cumpără niciun bilet nu are nicio șansă de câștig, iar probabilitatea sa teoretică este determinată după cum urmează:
P (0) = 0 / 1.000 = 0 = 0%
Ai o monedă cu scump pe o parte și scut sau ștampila pe de altă parte. Când este aruncată moneda, care este probabilitatea teoretică că va apărea în cap??
P (scump) = n (scump) / N ( față + scut ) = ½ = 0,5 = 50%
Rezultatul este interpretat după cum urmează: dacă s-ar face un număr mare de aruncări, în medie, la fiecare 2 aruncări, una dintre ele ar da capete.
În termeni procentuali, interpretarea rezultatului este că efectuarea unui număr infinit mare de aruncări, în medie din 100 dintre ele 50 ar duce la capete.
Într-o cutie sunt 3 baloane albastre, 2 baloane roșii și 1 verde. Care este probabilitatea teoretică ca atunci când scoți o marmură din cutie să fie roșie?
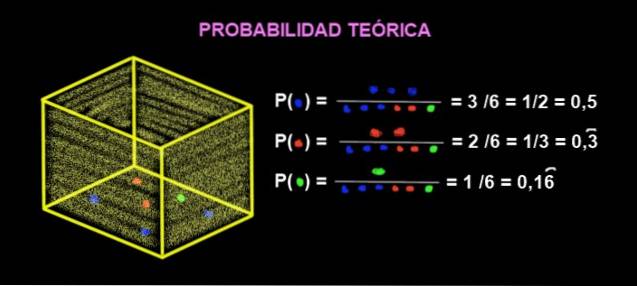
Probabilitatea ca acesta să iasă roșu este:
P (roșu) = Numărul de cazuri favorabile / Numărul de cazuri posibile
Și anume:
P (roșu) = Numărul de baloane roșii / Numărul total de baloane
În cele din urmă, probabilitatea ca o marmură roșie să fie desenată este:
P (roșu) = 2/6 = ⅓ = 0,3333 = 33,33%
În timp ce probabilitatea ca atunci când trageți o marmură verde este:
P (verde) = ⅙ = 0,1666 = 16,66%
În cele din urmă, probabilitatea teoretică de a obține o marmură albastră într-o extracție oarbă este:
P (albastru) = 3/6 = ½ = 0,5 = 50%
Adică, pentru fiecare 2 încercări, rezultatul va fi albastru într-una dintre ele și o altă culoare în altă încercare, sub premisa că marmura extrasă este înlocuită și că numărul de încercări este foarte, foarte mare..
Determinați probabilitatea ca la aruncarea unei matrițe să se obțină o valoare mai mică sau egală cu 4.
Pentru a calcula probabilitatea apariției acestui eveniment, se va aplica definiția probabilității teoretice:
P (≤4) = Numărul de cazuri favorabile / Numărul de cazuri posibile
P (≤5) = 5/6 = = 83,33%
Găsiți probabilitatea ca la două aruncări consecutive ale unei matrițe normale cu șase fețe, 5 să se rostogolească de 2 ori.
Pentru a răspunde la acest exercițiu, este convenabil să creați un tabel care să arate toate posibilitățile. Prima cifră indică rezultatul primei matrițe și a doua rezultatul celeilalte.
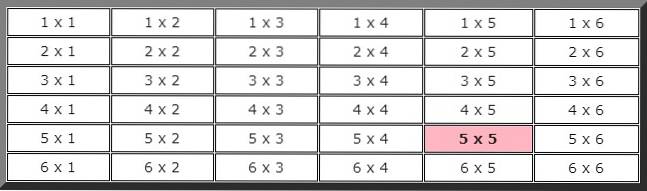
Pentru a calcula probabilitatea teoretică trebuie să cunoaștem numărul total de cazuri posibile, în acest caz, după cum se poate vedea din tabelul anterior, există 36 de posibilități.
De asemenea, observând tabelul, se poate deduce că numărul cazurilor favorabile evenimentului în care în cele două lansări consecutive iese 5 este doar 1, evidențiat cu culoare, prin urmare probabilitatea ca acest eveniment să apară este:
P (5 x 5) = 1/36.
Acest rezultat ar fi putut fi atins, de asemenea, utilizând una dintre proprietățile probabilității teoretice, care afirmă că probabilitatea combinată a două evenimente independente este produsul probabilităților lor individuale..
În acest caz, probabilitatea ca prima aruncare să ruleze 5 este ⅙. A doua aruncare este complet independentă de prima, prin urmare probabilitatea ca 5 să fie aruncată în a doua este, de asemenea, ⅙. Deci probabilitatea combinată este:
P (5 × 5) = P (5) P (5) = (1/6) (1/6) = 1/36.
Găsiți probabilitatea ca un număr mai mic de 2 să fie aruncat la prima aruncare și un număr mai mare de 2 să fie aruncat la a doua.
Din nou, trebuie construit un tabel cu eventuale evenimente, unde sunt evidențiate cele în care prima aruncare a fost mai mică de 2 și în a doua mai mare de 2..
În total există 4 posibilități dintr-un total de 36. Adică probabilitatea acestui eveniment este:
P (<2 ; >2) = 4/36 = 1/9 = 0,1111 = 11,11%
Folosind teorema probabilității care afirmă:
Probabilitatea apariției a două evenimente independente este egală cu produsul probabilităților individuale.
Se obține același rezultat:
P (<2) P(>2) = (1/6) (4/6) = 4/36 = 0.1111 = 11.11%
Valoarea obținută cu această procedură coincide cu rezultatul anterior, prin definiția teoretică sau clasică a probabilității.
Care este probabilitatea ca la aruncarea a două zaruri suma valorilor să fie de 7.
Pentru a găsi soluția în acest caz, a fost întocmit un tabel de posibilități în care cazurile care îndeplinesc condiția ca suma valorilor să fie 7 au fost indicate în culoare.
Privind tabelul, pot fi numărate 6 cazuri posibile, deci probabilitatea este:
P (I + II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%
Nimeni nu a comentat acest articol încă.