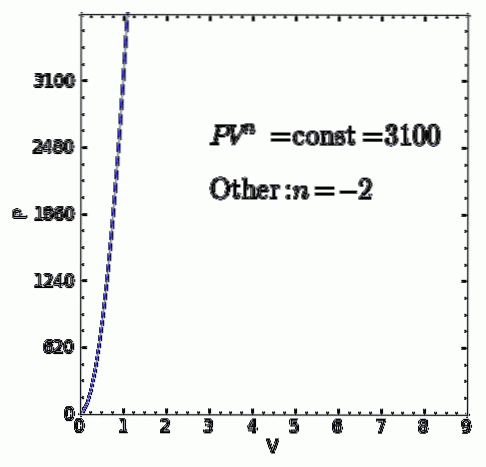
A proces poltropic este un proces termodinamic care apare atunci când relația dintre presiune P iar volumul V dat de P.Vn rămâne constantă. Exponentul n este un număr real, în general între zero și infinit, dar în unele cazuri poate fi negativ.
Valoarea a n primește numele de indice de poltropie și este important să subliniem faptul că în timpul unui proces termodinamic poltropic, indicele respectiv trebuie să mențină o valoare fixă, altfel procesul nu va fi considerat poltropic.
Indice articol
Unele cazuri caracteristice ale proceselor poltropice sunt:
- Procesul izotermic (la temperatura constantă T), în care exponentul este n = 1.
- Un proces izobaric (la presiune constantă P), în acest caz n = 0.
- Procesul izocoric (la volum constant V), pentru care n = + ∞.
- Procese adiabatice (la entropie constantă S), în care exponentul este n = γ, unde γ este constanta adiabatică. Această constantă este coeficientul dintre capacitatea de căldură la presiune constantă Cp împărțit la capacitatea de căldură la volum constant Cv:
γ = Cp / Cv
- Orice alt proces termodinamic care nu este unul dintre cazurile anterioare. dar asta se conformează P.Vn = ctte cu indice poltropic real și constant n va fi, de asemenea, un proces poltropic.
Una dintre principalele aplicații ale ecuației poltropice este calcularea muncii efectuate de un sistem termodinamic închis, atunci când trece de la o stare inițială la o stare finală într-un mod cvasistatic, adică în urma unei succesiuni de stări de echilibru..
Lucrarea mecanică W efectuată de un sistem termodinamic închis este calculată prin expresia:
W = ∫P.dV
Unde P este presiunea și V volumul.
Ca și în cazul unui proces poltropic, relația dintre presiune și volum este:
P.V n = constantă = C
Rezolvarea pentru P din expresia anterioară pentru a o înlocui în expresia de lucru:
P = C /V n
Avem lucrările mecanice efectuate în timpul unui proces poltropic, care începe într-o stare inițială 1 și se termină în starea finală 2. Toate acestea apar în următoarea expresie:
C = P1 V1n = PDouă VDouăn
Prin substituirea valorii constantei în expresia de lucru, obținem:
W = (PDouă VDouă - P1 V1) / (1-n)
În cazul în care substanța de lucru poate fi modelată ca un gaz ideal, avem următoarea ecuație de stare:
P.V = m.R.T
Unde m este numărul de moli ai gazului ideal și R este constanta gazului universal.
Pentru un gaz ideal care urmează un proces poltropic cu un indice de poltropie diferit de unitate și care trece dintr-o stare cu temperatura inițială T1 într-o altă stare cu temperatura TDouă avem că munca depusă este dată de următoarea formulă:
W = m R (TDouă - T1) / (1-n)
Conform formulei lucrării obținute în secțiunea anterioară, avem că lucrarea unui proces poltropic cu n = ∞ este nulă, deoarece expresia lucrării este împărțită la infinit și, prin urmare, rezultatul tinde la zero.
O altă modalitate de a ajunge la acest rezultat este din relația P1 V1n = PDouă VDouăn, care poate fi rescris după cum urmează:
(P1/ PDouă) = (VDouă/ V1)n
Luând a n-a rădăcină în fiecare membru, obținem:
(VDouă/ V1) = (P1/ PDouă)(1 / n)
În cazul în care n → ∞, avem (VDouă/ V1) = 1, ceea ce înseamnă că:
VDouă = V1
Adică, volumul nu se schimbă într-un proces poltropic cu n → ∞. Prin urmare, diferențialul de volum dV în integralul muncii mecanice este 0. Aceste tipuri de procese poltropice sunt cunoscute și sub denumirea de procese izocoric, sau procese de volum constant.
Din nou avem expresia expresie pentru muncă:
W = ∫P dV
În cazul unui proces poltropic cu n = 1, relația dintre presiune și volum este:
P V = constantă = C
Rezolvând P din expresia anterioară și înlocuind, avem treaba făcută pentru a trece de la starea inițială 1 la starea finală 2:
Și anume:
W = C ln (VDouă/ V1).
Deoarece stările inițiale și finale sunt bine determinate, așa va fi și ctte. Și anume:
C = P1 V1 = PDouă VDouă
În cele din urmă, avem următoarele expresii utile pentru a găsi lucrul mecanic al unui sistem închis poltropic în care n = 1.
W = P1 V1 ln (VDouă/ V1) = PDouă VDouă ln (VDouă/ V1)
Dacă substanța de lucru constă din m moli de gaz ideal, atunci se poate aplica ecuația de stare a gazului ideal: P V = m.R.T.
În acest caz, așa cum P.V1 = ctte, avem că un proces poltropic cu n = 1 este un proces la temperatură constantă T (izotermă), astfel încât să poată fi obținute următoarele expresii pentru lucrare:
W = m R T1 ln (VDouă/ V1) = m R TDouă ln (VDouă/ V1)
Să presupunem că un cilindru cu un piston mobil umplut cu un kilogram de aer. Inițial aerul ocupă un volum V1= 0,2 m3 la o presiune P1= 400 kPa. Se urmărește un proces poltropic cu n = γ = 1,4, a cărui stare finală are presiune PDouă = 100 kPa. Determinați munca efectuată de aer pe piston.
Când indicele de poltropie este egal cu constanta adiabatică, există un proces în care substanța de lucru (aerul) nu schimbă căldura cu mediul și, prin urmare, entropia nu se schimbă..
Pentru aer, un gaz ideal diatomic, avem:
γ = Cp / Cv, cu Cp = (7/2) R și Cv = (5/2) R
Atunci:
γ = 7/5 = 1,4
Folosind expresia procesului poltropic, volumul final al aerului poate fi determinat:
VDouă = [(PDouă V11.4) / PDouă](1 / 1.4) = 0,54 m3.
Acum avem condițiile pentru a aplica formula pentru munca realizată într-un proces poltropic pentru n ≠ 1 obținut mai sus:
W = (PDouă VDouă - P1 V1) / (1-n)
Înlocuind valorile corespunzătoare avem:
W = (100 kPa 0,54 m3 - 400 kPa 0,2 m3) / (1 - 1,4) = 65,4 kJ
Să presupunem același cilindru din Exemplul 1, cu un piston mobil umplut cu un kilogram de aer. Inițial, aerul ocupă un volum V1 = 0,2 m3 la o presiune P1 = 400 kPa. Dar, spre deosebire de cazul anterior, aerul se extinde izoterm pentru a atinge o presiune finală P2 = 100 kPa. Determinați munca efectuată de aer pe piston.
După cum s-a văzut anterior, procesele izoterme sunt procese poltropice cu indicele n = 1, deci este adevărat că:
P1 V1 = P2 V2
În acest fel, volumul final poate fi ușor decojit pentru a obține:
V2 = 0,8 m3
Apoi, folosind expresia de lucru obținută anterior pentru cazul n = 1, avem că munca efectuată de aer pe piston în acest proces este:
W = P1 V1 ln (V2 / V1) = 400000 Pa × 0,2 m3 ln (0,8 / 0,2) = 110,9 kJ.
Nimeni nu a comentat acest articol încă.