
Programare liniară pentru ce este, modele, constrângeri, aplicații
programare liniară este o metodă matematică utilizată pentru a optimiza (maximiza sau minimiza după cum este necesar) o funcție ale cărei variabile sunt supuse restricțiilor, atâta timp cât funcția și restricțiile sunt liniar dependente de variabile.
În general, funcția care trebuie optimizată modelează o situație practică, cum ar fi profitul unui producător ale cărui intrări, forță de muncă sau utilaje sunt limitate.

Unul dintre cele mai simple cazuri este cel al unei funcții liniare care trebuie maximizată, care depinde doar de două variabile, numite variabile de decizie. Poate avea forma:
Z = k1x + kDouăDa
Cu k1 și kDouă constant. Această funcție este cunoscută sub numele de Funcție obiectivă. Desigur, există situații care merită mai mult de două variabile pentru studiu, fiind mai complexe:
Z = k1X1 + kDouăXDouă + k3X3 +... .
Iar constrângerile sunt, de asemenea, modelate matematic de un sistem de ecuații sau inegalități, la fel de liniar în X și Da.
Setul de soluții ale acestui sistem se numește soluții fezabile sau puncte fezabile. Și printre punctele fezabile există cel puțin unul, care optimizează funcția obiectivă.
Programarea liniară a fost dezvoltată independent de fizicianul și matematicianul american George Dantzig (1914-2005) și de matematicianul și economistul rus Leonid Kantorovich (1912-1986) la scurt timp după al doilea război mondial..
Metoda de depanare cunoscută sub numele de metoda simplex Este ideea lui Dantzig, care a lucrat pentru Forțele Aeriene ale SUA, Universitatea din Berkeley și Universitatea Stanford.

Indice articol
- 1 Modele de programare liniară
- 2 Exemplu de model
- 3 Metode de soluție
- 3.1 - Metoda grafică sau geometrică
- 3.2 - Metoda simplex a lui Dantzig
- 4 Aplicații
- 5 Exerciții rezolvate
- 5.1 - Exercițiul 1
- 5.2 - Exercițiul 2
- 6 Referințe
Modele de programare liniară
Elementele necesare pentru stabilirea unui model de programare liniar, adecvat unei situații practice, sunt:
-Funcție obiectivă
-Variabile de decizie
-Restricții
În funcția obiectivă definiți ce doriți să realizați. De exemplu, să presupunem că doriți să vă maximizați profiturile din fabricarea anumitor produse. Apoi se stabilește funcția „profit”, în funcție de prețul la care sunt vândute produsele.
În termeni matematici, această funcție poate fi exprimată abreviat folosind notația de însumare:
Z = ∑keu Xeu
În această ecuație, keu sunt coeficienți și xeu sunt variabilele de decizie.
Variabilele de decizie sunt elementele sistemului al căror control este avut și valorile lor sunt numere reale pozitive. În exemplul propus, variabilele de decizie sunt cantitatea fiecărui produs care urmează să fie fabricat pentru a obține profitul maxim.
În cele din urmă, avem constrângerile, care sunt ecuații liniare sau inegalități în ceea ce privește variabilele de decizie. Acestea descriu limitările problemei, care sunt cunoscute și pot fi, de exemplu, cantitățile de materie primă disponibile în fabricație..
Tipuri de restricții
Puteți avea un număr M de limitări, începând de la j = 1 pana cand j = M. Matematic, restricțiile sunt de trei tipuri:
- LAj = ∑ aij . Xeu
- Bj ≥ ∑ bij . Xeu
- Cj ≤ ∑ cij . Xeu
Prima restricție este de tipul ecuației liniare și înseamnă că valoarea Aj, ceea ce se știe, trebuie respectat.
Restul de două constrângeri sunt inegalități liniare și înseamnă că valorile B.j și Cj, cunoscute, pot fi respectate sau depășite, atunci când simbolul afișat este ≥ (mai mare sau egal cu) sau respectat sau nu depășit, dacă simbolul este ≤ (mai mic sau egal cu).
Exemplu de model
Domeniile de aplicare sunt foarte diverse, variind de la administrarea afacerilor la nutriție, dar pentru a înțelege metoda, un model simplu al unei situații practice cu două variabile este propus mai jos..
O patiserie locală este cunoscută pentru două specialități: tortul din pădurea neagră și tortul sacripantina..
La prepararea ei au nevoie de ouă și zahăr. Pentru pădurea neagră aveți nevoie de 9 ouă și 500 g zahăr, în timp ce pentru sacripantină aveți nevoie de 8 ouă și 800 g zahăr. Prețurile de vânzare respective sunt de 8 USD și 10 USD.
Problema este: Câte prăjituri de fiecare tip trebuie să facă patiseria pentru a-și maximiza profitul, știind că are 10 kilograme de zahăr și 144 de ouă?
Variabile de decizie
Variabilele de decizie sunt „x” și „y”, care iau valori reale:
-x: numărul prăjiturilor din pădurea neagră
-și: prăjiturile de tip sacripantina.
Restricții
Restricțiile sunt date de faptul că numărul prăjiturilor este o cantitate pozitivă și există cantități limitate de materie primă pentru a le prepara..
Prin urmare, în formă matematică, aceste restricții iau forma:
- x ≥ 0
- și ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8y ≤ 10
Constrângerile 1 și 2 constituie condiție de non-negativitate expuse anterior și toate inegalitățile ridicate sunt liniare. În restricțiile 3 și 4 sunt valorile care nu trebuie depășite: 144 ouă și 10 kg zahăr.
Funcție obiectivă
În cele din urmă, funcția obiectivă este profitul obținut la fabricarea cantității „x” de prăjituri din pădurea neagră plus cantitatea „y” de sacripantine. Se construiește înmulțind prețul cu cantitatea de prăjituri făcute și adăugând pentru fiecare tip. Este o funcție liniară pe care o vom numi G (x, y):
G = 8x + 10y
Metode de soluționare
Diferitele metodologii de soluție includ metode grafice, algoritmul simplex și metoda punctului interior, pentru a numi câteva..
- Metoda grafică sau geometrică
Când aveți o problemă cu două variabile precum cea din secțiunea anterioară, constrângerile determină o regiune poligonală în plan X y, apel regiune fezabilă sau regiunea de viabilitate.
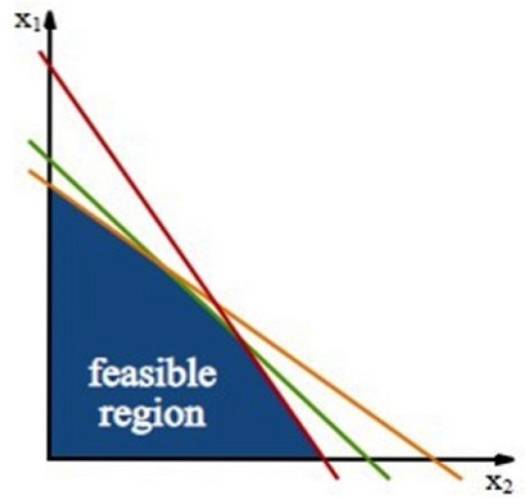
Această regiune este construită prin intermediul linii de restricție, care sunt liniile obținute din inegalitățile constrângerilor, lucrând numai cu semnul egalității.
În cazul brutăriei care dorește să optimizeze profiturile, liniile de constrângere sunt:
- x = 0
- y = 0
- 9x + 8y = 144
- 0,5 x + 0,8y = 10
Toate punctele din regiunea cuprinsă de aceste linii sunt soluții posibile, deci există infinit multe dintre ele. Cu excepția cazului în care regiunea fezabilă se dovedește a fi goală, caz în care problema pusă nu are nicio soluție.
Din fericire, pentru problema patiseriei regiunea fezabilă nu este goală, o avem mai jos.
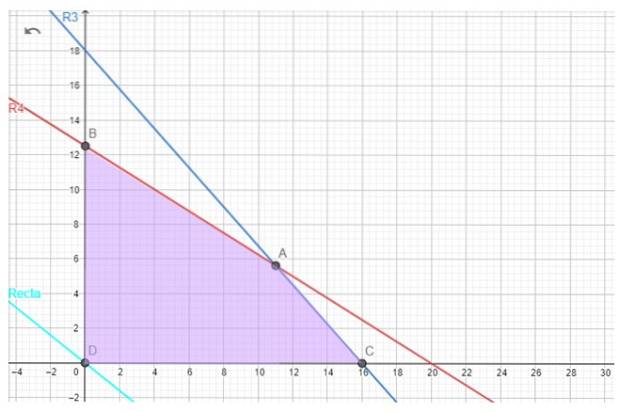
Soluția optimă, dacă există, se găsește cu ajutorul funcției obiective. De exemplu, când încercăm să găsim câștigul maxim G, avem următoarea linie, care se numește linia iso-profit:
G = k1x + kDouăy → y = -k1x / kDouă + G / kDouă
Cu această linie obținem toate perechile (x, y) care oferă un câștig dat G, deci există o familie de linii în funcție de valoarea lui G, dar toate cu aceeași pantă -k1 / kDouă, deci sunt linii paralele.
Soluția optimă
Acum, se poate arăta că soluția optimă a unei probleme liniare este întotdeauna un punct extrem sau un vârf al regiunii fezabile. Atunci:
Linia de soluție este cea mai îndepărtată de origine și are cel puțin un punct în comun cu regiunea fezabilă.
Dacă linia cea mai apropiată de origine are un întreg segment în comun cu regiunea fezabilă, se spune că există soluții infinite. Acest caz apare dacă panta liniei izo-profit este egală cu cea a oricăreia dintre celelalte linii care limitează regiunea.
Pentru patiseria noastră, vârfurile candidate sunt A, B și C.
- Metoda simplă a lui Dantzig
Metoda grafică sau geometrică este aplicabilă pentru două variabile. Cu toate acestea, este mai complicat atunci când există trei variabile și este imposibil de utilizat pentru un număr mai mare de variabile..
Când se tratează probleme cu mai mult de două variabile, metoda simplex, care constă dintr-o serie de algoritmi pentru optimizarea funcțiilor obiective. Matricele și aritmetica simplă sunt adesea folosite pentru efectuarea calculelor.
Metoda simplex începe prin alegerea unei soluții fezabile și verificarea dacă este optimă. Dacă este, am rezolvat deja problema, dar dacă nu, continuăm spre o soluție mai aproape de optimizare. Dacă soluția există, algoritmul o găsește în câteva încercări.
Aplicații
Programarea liniară și neliniară sunt aplicate în multe domenii pentru a lua cele mai bune decizii în ceea ce privește reducerea costurilor și creșterea profiturilor, care nu sunt întotdeauna monetare, deoarece pot fi măsurate în timp, de exemplu, dacă doriți să minimizați timpul necesar să efectueze o serie de operațiuni.
Iată câteva câmpuri:
-În marketing este folosit pentru a găsi cea mai bună combinație de media (rețele sociale, televiziune, presă și altele) pentru a face publicitate unui anumit produs.
-Pentru atribuirea sarcinilor adecvate personalului unei companii sau fabrici sau a programelor acestora.
-În selectarea celor mai hrănitoare alimente și la cel mai mic cost în industria animalelor și a păsărilor.
Exerciții rezolvate
- Exercitiul 1
Rezolvați grafic modelul de programare liniar ridicat în secțiunile precedente.
Soluţie
Este necesar să graficăm setul de valori determinat de sistemul de constrângeri specificat în problemă:
- x ≥ 0
- și ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8y ≤ 10
Regiunea dată de inegalitățile 1 și 2 corespunde primului cadran al planului cartezian. În ceea ce privește inegalitățile 3 și 4, începem prin a găsi liniile de restricție:
9x + 8y = 144
0,5 x + 0,8y = 10 → 5x + 8y = 100
Regiunea fezabilă este un patrulater ale cărui vârfuri sunt punctele A, B, C și D.
Profitul minim este 0, prin urmare linia 8x + 10y = 0 este limita inferioară, iar liniile iso-profit au panta -8/10 = - 0,8.
Această valoare este diferită de pantele celorlalte linii de restricție și întrucât regiunea fezabilă este delimitată, există soluția unică.
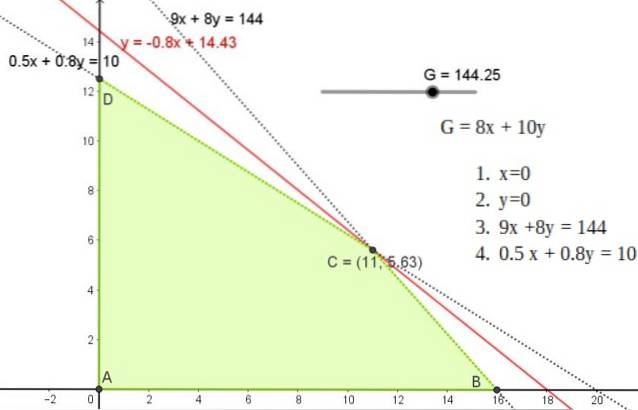
Această soluție corespunde unei linii cu panta -0,8 care trece prin oricare dintre punctele A, B sau C, ale căror coordonate sunt:
A (11; 5.625)
B (0; 12,5)
C (16, 0)
Soluție optimă
Calculăm valoarea lui G pentru fiecare dintre aceste puncte:
-(11; 5.625): GLA = 8 x 11 + 10 x 5.625 = 144,25
-(0; 12,5): GB = 8 x 0 + 10 x 12,5 = 125
-(16, 0): GC = 8 x 16 + 10 x 0 = 128
Cel mai mare profit se găsește producând 11 prăjituri din pădurea neagră și 5.625 prăjituri sacripantine. Această soluție se potrivește cu cea găsită prin intermediul software-ului.
- Exercițiul 2
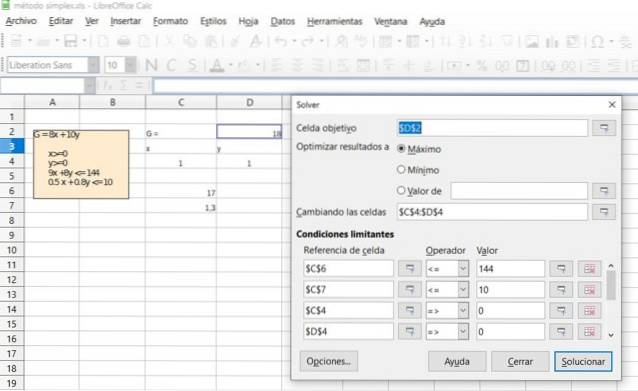
Verificați rezultatul exercițiului anterior utilizând funcția Solver disponibilă în majoritatea foilor de calcul precum Excel sau LibreOffice Calc, care încorporează algoritmul Simplex pentru optimizare în programarea liniară.
Soluţie
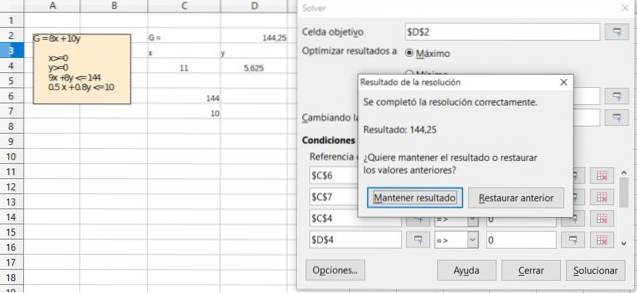
Referințe
- Sclipitor. Programare liniară. Recuperat de pe: brilliant.org.
- Eppen, G. 2000. Operations Research in Administrative Science. Al 5-lea. Ediție. Prentice hall.
- Haeussler, E. 1992. Matematică pentru management și economie. Al 2-lea. Ediție. Grupo Editorial Iberoamericana.
- Hiru.eus. Programare liniară. Recuperat de la: hiru.eus.
- Wikipedia. Programare liniară. Recuperat din: es. wikipedia.org.


Nimeni nu a comentat acest articol încă.