Care este modulul de forfecare, rigiditate sau forfecare? (Exerciții rezolvate)

modul de tăiere descrie răspunsul unui material la aplicarea unei solicitări de forfecare care îl deformează. Alte denumiri frecvent utilizate pentru modulul de forfecare sunt modulul de forfecare, modulul de forfecare, elasticitatea transversală sau elasticitatea tangențială..

Când tensiunile sunt mici, deformările sunt proporționale cu ele, conform legii lui Hooke, modulul de forfecare fiind constanta proporționalității. Prin urmare:

Modul de forfecare = Stres de forfecare / Tensiune

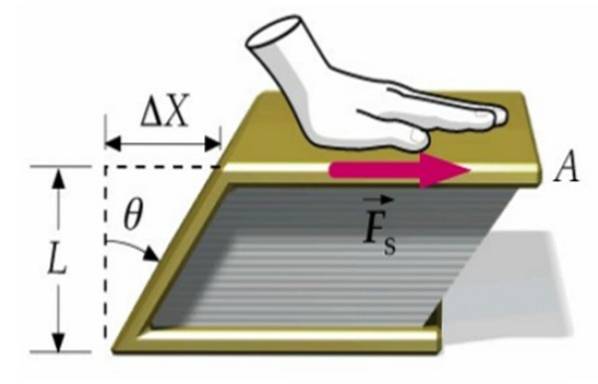
Să presupunem că o forță este aplicată pe coperta unei cărți, cealaltă fiind fixată pe suprafața mesei. În acest fel, cartea în ansamblu nu se mișcă, ci se deformează atunci când capacul superior se mișcă față de cel inferior cu cantitatea Δx.

Cartea trece de la o secțiune transversală dreptunghiulară la o secțiune în formă de paralelogram, așa cum vedem în imaginea de mai sus.

Fi:

τ = F / A

Stresul sau tensiunea de forfecare, fiind F magnitudinea forței aplicate și LA zona asupra căreia acționează.

Deformarea cauzată este dată de coeficientul:

δ = Δx / L

Prin urmare, modulul de forfecare, pe care îl vom denumi G, este:

Și, din moment ce Δx / L nu are dimensiuni, unitățile lui G sunt aceleași cu tensiunea de forfecare, care este raportul forță / suprafață..

În sistemul internațional de unități, aceste unități sunt Newton / metru pătrat sau pascal, prescurtat Pa. Iar în unitățile anglo-saxone este lira / inch pătrat, prescurtat psi.

Indice articol

• 1 Modul de tăiere pentru diverse materiale
  • 1.1 Măsurarea experimentală a modulului de forfecare
  • 1.2 Cum se găsește G?
• 2 Exerciții cu soluție
  • 2.1 - Exercițiul 1
  • 2.2 - Exercițiul 2
• 3 Referințe

Modul de tăiere pentru diverse materiale

Sub acțiunea forțelor de forfecare precum cele descrise, obiectele oferă o rezistență similară cu cea a cărții, în care straturile interioare alunecă. Acest tip de deformare poate apărea numai în corpuri solide, care au o rigiditate suficientă pentru a rezista la deformare..

Pe de altă parte, lichidele nu oferă acest tip de rezistență, dar pot suferi deformări ale volumului.

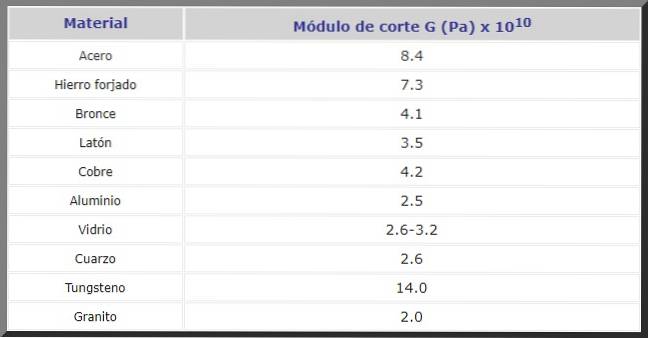
Mai jos este modulul de tăiere G în Pa pentru diverse materiale utilizate frecvent în construcții și la fabricarea mașinilor și pieselor de schimb de toate tipurile:

Măsurarea experimentală a modulului de forfecare

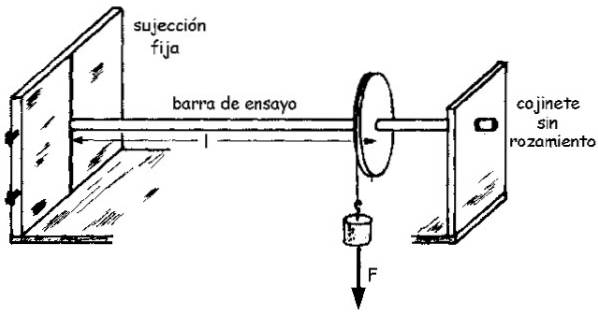
Pentru a găsi valoarea modulului de forfecare, probele din fiecare material trebuie testate și răspunsul lor la aplicarea unei solicitări de forfecare..

Proba este o tijă din material, cu rază R și lungimea L cunoscut, care este fixat la un capăt, în timp ce celălalt este conectat la arborele unei scripete libere să se rotească.

Scripetele este legat cu o frânghie, la capătul liber al căruia se atârnă o greutate care exercită o forță F pe tija prin frânghie. Și această forță produce la rândul ei un moment M pe tijă, care apoi rotește un unghi mic θ.

O diagramă a ansamblului poate fi văzută în următoarea figură:

Magnitudinea momentului M, pe care le denotăm ca fiind M (fără caractere aldine) este legat de unghiul rotit θ prin modulul de forfecare G conform următoarei ecuații (dedusă printr-o integrală simplă):

Deoarece magnitudinea momentului este egală cu produsul modulului de forță F și raza fuliei R_p:

M = F.R_p

Iar puterea este greutatea care atârnă W, atunci:

M = W.R_p

Înlocuind în ecuație magnitudinea momentului:

Există relația dintre greutate și unghi:

Cum se găsește G?

Această relație între variabile W Da θ este liniar, deci se măsoară diferitele unghiuri produse de agățarea unor greutăți diferite.

Perechile de greutate și unghiuri sunt reprezentate pe hârtie milimetrică, se montează cea mai bună linie care trece prin punctele experimentale și se calculează panta. m a liniei respective.

Exerciții cu soluție

- Exercitiul 1

La un capăt este fixată o tijă de 2,5 metri lungime și o rază de 4,5 mm. Cealaltă este conectată la o scripete cu raza de 75 cm care are o greutate de agățare W de 1,3 kg. Unghiul rotit este de 9,5º.

Cu aceste date, se solicită calcularea modulului de forfecare G al tijei.

Soluţie

Din ecuație:

G este șters:

Și valorile date în declarație sunt substituite, având grijă să exprimăm toate datele din Sistemul Internațional de Unități SI:

R = 4,5 mm = 4,5 x 10 ^-3 m

R_p = 75 cm = 0,075

Pentru a trece de la kilograme (care sunt de fapt kilograme - forță) la newton înmulțiți cu 9,8:

L = 1,3 kg-forță = 1,3 x 9,8 N = 12,74 N

Și, în cele din urmă, gradele trebuie să fie în radiani:

9,5 º = 9,5 x2π / 360 radiani = 0,1665 radiani.

Cu toate acestea aveți:

= 2.237 x 10¹⁰ Pa

- Exercițiul 2

Un cub din gel are o latură de 30 cm. Una dintre fețele sale este fixă, dar în același timp, o forță paralelă de 1 N se aplică feței opuse, care datorită acesteia se mișcă 1 cm (vezi exemplul cărții din figura 1).

Se solicită calcularea cu aceste date:

a) Mărimea tensiunii de forfecare

b) Tulpina δ

c) Valoarea modulului de forfecare

Solutie la

Mărimea tensiunii de forfecare este:

τ = F / A

Cu:

A = latură^Două = (30 x 10^-Două cm)^Două = 0,09 m^Două

Prin urmare:

τ = 1 N / 0,09 m^Două = 11,1 Pa

Soluția b

Tulpina nu este alta decât valoarea lui δ, dată de:

δ = Δx / L

Deplasarea feței supuse forței este de 1 cm, apoi:

δ = 1/30 = 0,0333

Soluția c

Modulul de forfecare este coeficientul dintre tensiunea de forfecare și tensiunea:

G = Stres de forfecare / Tensiune

Prin urmare:

G = 11,1 Pa / 0,033 = 336,4 Pa

Referințe

1. Bere, F. 2010. Mecanica materialelor. McGraw Hill. Al 5-lea. Ediție.
2. Franco García, A. Solid Rigid. Măsurarea modulului de forfecare. Recuperat de pe: sc.ehu.es.
3. Giancoli, D. 2006. Fizică: principii cu aplicații. Al 6-lea. Ed prentice hall.
4. Resnick, R. (1999). Fizic. Vol. 1. Ediția a 3-a. În spaniolă. Compañía Editorial Continental S.A. de C.V.
5. Universitatea din Valladolid. Departamentul de fizică a materiei condensate. Selectarea problemelor. Recuperat de pe: www4.uva.es.