
Care este momentul magnetic?
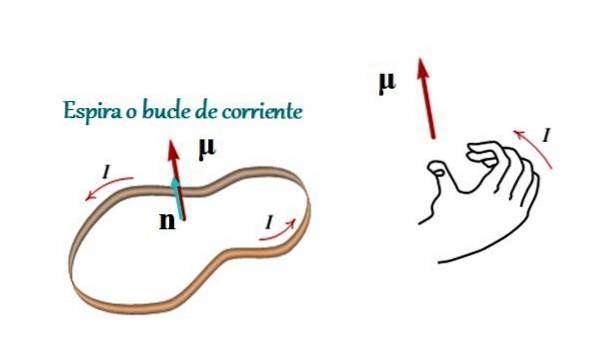
moment magnetic este un vector care leagă curentul care trece printr-o buclă sau buclă închisă cu aria sa. Modulul său este egal cu produsul intensității curentului și zonei, iar direcția și sensul său sunt date de regula din dreapta, așa cum se arată în figura 1.
Această definiție este valabilă indiferent de forma buclei. În ceea ce privește unitatea momentului magnetic, în Sistemul Internațional al unităților SI este Ampere × mDouă.
În termeni matematici, denotând vectorul moment magnetic cu litera greacă μ (cu caractere aldine, deoarece este un vector și astfel se distinge de magnitudinea sa), este exprimat ca:
μ = AI n
Unde I este intensitatea curentului, A este aria închisă de buclă și n este vectorul unitar (cu un modul egal cu 1) care indică direcția perpendiculară pe planul buclei și al cărui sens este dat de regula degetului mare drept (a se vedea figura 1).
Această regulă este foarte simplă: prin curbarea celor patru degete ale mâinii drepte pentru a urma curentul, degetul mare indică direcția și sensul de direcție. n și deci cel al momentului magnetic.
Ecuația de mai sus este valabilă pentru o buclă. Dacă există N spire ca într-o bobină, momentul magnetic este înmulțit cu N:
μ = NAI n
Indice articol
- 1 Moment magnetic și câmp magnetic
- 1.1 Câmpul magnetic al dipolului
- 2 Efectul unui câmp extern asupra buclei
- 2.1 Cuplul pe o buclă dreptunghiulară
- 2.2 Energia potențială a dipolului magnetic
- 3 Referințe
Moment magnetic și câmp magnetic
Este ușor să găsiți expresii pentru momentul magnetic al virajelor cu forme geometrice regulate:
-Întoarcere pătrată laterală side: μ = EuℓDouă n
-Spirala dreptunghiulară a laturilor la Da b: μ = Iab n
-Spirală circulară cu rază R: μ = IπRDouă n
Câmp magnetic dipol
Câmpul magnetic produs de bucla sau bucla de curent este foarte asemănător cu cel al unui magnet magnetic și, de asemenea, cu cel al Pământului.
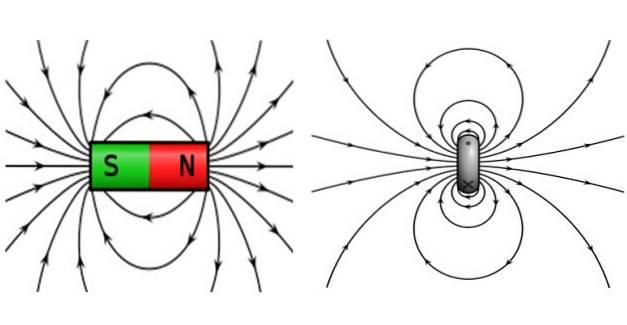
Magneții cu bare sunt caracterizați prin faptul că au un pol nord și un pol sud, unde polii opuși atrag și ca polii se resping. Liniile de câmp sunt închise, părăsesc polul nord și ajung la polul sud.
Acum, polii magnetici sunt inseparabili, ceea ce înseamnă că, dacă împărțiți un magnet cu bare în doi magneți mai mici, aceștia au în continuare proprii poli nordici și sudici. Nu este posibil să aveți poli magnetici izolați, de aceea se numește magnetul barei dipol magnetic.
Câmpul magnetic al unei bucle circulare de rază R, purtând un curent I, este calculat folosind legea Biot-Savart. Pentru punctele aparținând axei sale de simetrie (în acest caz axa x), câmpul este dat de:

Relația dintre câmpul magnetic și momentul magnetic al dipolului
Includerea momentului magnetic în rezultatele expresiei anterioare:

În acest fel, intensitatea câmpului magnetic este proporțională cu momentul magnetic. Rețineți că intensitatea câmpului scade odată cu cubul distanței.
Această aproximare este aplicabilă oricărei bucle, atâta timp cât X este mare comparativ cu dimensiunile sale.
Și întrucât liniile acestui câmp sunt atât de similare cu cele ale magnetului barei, ecuația este un model bun pentru acest câmp magnetic și pentru celelalte sisteme ale căror linii sunt similare, cum ar fi:
-Particulele încărcate în mișcare ca electronul.
-Atomul.
-Pământul și alte planete și sateliți ai sistemului solar.
-Stele.
Efectul unui câmp extern asupra buclei
O caracteristică foarte importantă a momentului magnetic este legătura sa cu cuplul pe care bucla îl experimentează în prezența unui câmp magnetic extern..
Un motor electric conține bobine prin care trece un curent de direcție schimbătoare și care, datorită câmpului extern, experimentează un efect de rotire. Această rotație face ca o axă să se miște și energia electrică este transformată în energie mecanică în timpul procesului..
Cuplați pe o buclă dreptunghiulară
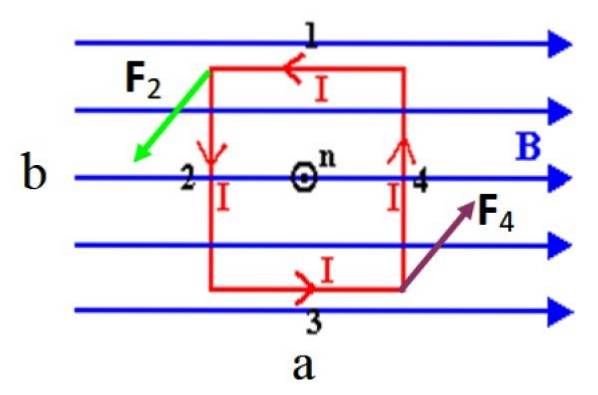
Să presupunem, pentru ușurința calculelor, o buclă dreptunghiulară cu laturile la Da b, al cărui vector normal n, proiectându-se către ecran, inițial perpendicular pe un câmp magnetic uniform B, ca în figura 3. Laturile buclei experimentează forțele date de:
F = EuL X B
Unde L este un vector de magnitudine egal cu lungimea segmentului și direcționat în funcție de curent, I este intensitatea acestuia și B este câmpul. Forța este perpendiculară pe ambele L în ceea ce privește câmpul, dar nu toate părțile experimentează forța.

În figura prezentată, nu există forță pe laturile scurte 1 și 3 deoarece acestea sunt paralele cu câmpul, amintiți-vă că produsul încrucișat între vectori paraleli este zero. Cu toate acestea, laturile lungi 2 și 4, care sunt perpendiculare pe B, experimentați forțele denumite ca FDouă Da F4.
Aceste forțe se formează o pereche: au aceeași magnitudine și direcție, dar direcții opuse, prin urmare nu sunt capabili să transfere bucla în mijlocul câmpului. Dar ei îl pot roti, de la cuplu τ exercitat de fiecare forță, în raport cu axa verticală care trece prin centrul buclei, are aceeași direcție și sens.
Conform definiției cuplului, unde r este vectorul de poziție:
τ = r X F
Atunci:
τDouă = τ4=(a / 2) F (+j )
Cuplurile individuale nu sunt anulate, deoarece au aceeași direcție și sens, așa că se adaugă:
τnet = τDouă + τ4 = a F (+j )
Și fiind magnitudinea forței F = IbB, rezultă:
τnet = I⋅a⋅b⋅B (+j )
Produsul a⋅b este zona A a buclei, deci Iab este magnitudinea momentului magnetic μ. Prin urmare τnet = μ⋅B (+j )
Se poate vedea că, în general, cuplul coincide cu produsul vector dintre vectori μ Da B:
τnet = μ X B
Și, deși această expresie a fost derivată pornind de la o buclă dreptunghiulară, este valabilă pentru o buclă plană de formă arbitrară.
Efectul câmpului asupra buclei este un cuplu care tinde să alinieze momentul magnetic cu câmpul.
Energia potențială a dipolului magnetic
Pentru a roti bucla sau dipolul în mijlocul câmpului, trebuie lucrat împotriva forței magnetice, care schimbă energia potențială a dipolului. Variația energiei ΔU, când rotația se rotește de la unghiul θsau unghiul θ este dat de integral:

ΔU = -μB cos θ
Care la rândul său poate fi exprimat ca produs punct între vectori B Da μ:
ΔU = - μB
Energia potențială minimă din dipol apare atunci când cos θ = 1, ceea ce înseamnă că μ Da B sunt paralele, energia este maximă dacă sunt opuse (θ = π) și este zero atunci când sunt perpendiculare (θ = π / 2).
Referințe
- Figueroa, D. 2005. Seria: Fizică pentru științe și inginerie. Volumul 5. Electromagnetismul. Editat de Douglas Figueroa (USB).
- Resnick, R. 1999. Fizică. Vol. 2. Ediția a 3-a. În spaniolă. Compañía Editorial Continental S.A. de C.V.
- Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 2. Pearson.
- Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 2. 7. Ed. Cengage Learning.
- Tipler, P. (2006) Fizică pentru știință și tehnologie. Ediția a 5-a Volumul 2. Editorial Reverté.


Nimeni nu a comentat acest articol încă.