
Ce sunt numerele triunghiulare? Proprietăți și demonstrații

Este cunoscut sub numele de numere triunghiulare la succesiunea numerelor care se obțin făcând o aranjare sau o figură de puncte sub forma unui triunghi echilateral. Primele din secvență sunt: 1, 3, 6, 10, 15, 21, ...
Primul număr triunghiular este 1, al doilea este 3, deoarece se obține prin adăugarea unui rând de două puncte la precedent, pentru a forma un triunghi echilateral de trei elemente.
Al treilea este 6, care apare atunci când se adaugă un rând de trei puncte la aranjamentul anterior, în așa fel încât se formează un triunghi de trei puncte pe fiecare latură. 10 al secvenței se obține prin adăugarea unui alt rând la aranjamentul anterior, astfel încât să se formeze un triunghi de patru puncte pe fiecare parte.
Formula care permite găsirea elementului n din secvența triunghiulară, cunoscut numărul triunghiular anterior este:
Tn = Tn-1 + n
Lista primelor șase numere triunghiulare se obține astfel:
-Primul: 1
-Al doilea: 1 + 2 = 3
-Al treilea: (1 +2) + 3 = 3 + 3 = 6
-Dormitor: (1 + 2 + 3) + 4 = 6 + 4 = 10
-a cincea: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15
-Şaselea: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21
Indice articol
- 1 Proprietățile numerelor triunghiulare
- 2 Demonstrații
- 2.1 - Demo 1
- 2.2 - Demo 2
- 2.3 - Demo 3
- 2.4 - Demonstrație 5
- 3 Referințe
Proprietățile numerelor triunghiulare
1.- Al n-lea număr triunghiular Tn al secvenței numerelor triunghiulare este jumătate din n înmulțit cu n + 1:
Tn = ½ n (n + 1)
2.- Suma numărului n-triunghiular cu numărul triunghiular anterior, adică (n-1) -th, este n pătrat:
Tn + Tn-1= nDouă
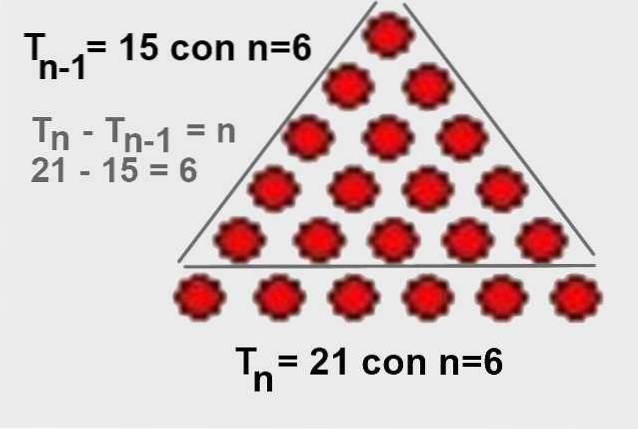
3.- Diferența numărului n-triunghiular minus al n-lea triunghiular minus este n:
Tn - Tn-1 = n
4.- Suma primelor n numere triunghiulare se numește numărul tetraedric Sn și este egală cu a șasea parte a produsului lui n înmulțit cu (n + 1) și înmulțit cu (n + 2):
Sn= ⅙ n (n + 1) (n + 2)
5.- Fiecare număr natural N este rezultatul sumei a trei numere triunghiulare:
N = Δ1 + Δ1 + Δ3
Această ultimă proprietate sau teoremă a fost descoperită de marele matematician Carl Friedrich Gauss în 1796, pe care a remarcat-o în jurnalul său plasând admirația greacă. Eureka! ce înseamnă "Am facut-o".
Acesta a fost același cuvânt folosit cu mult înainte de grecul Arhimede când a determinat greutatea aparentă a unui corp scufundat..
În această relație, numărul zero este luat ca triunghiular și poate exista repetare.
Demonstrații
- Demo 1
Dovediți că numărul triunghiular n-acest:
Tn = ½ n (n + 1)
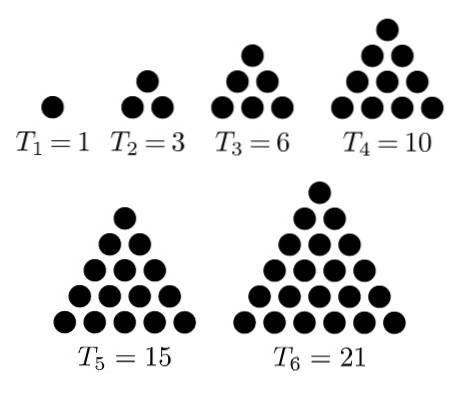
Este ușor să deducem formula de mai sus, dacă ne dăm seama că putem adăuga un număr egal de puncte aranjamentului triunghiular astfel încât să formeze un patrulater de puncte.
Deoarece numărul total de puncte din aranjamentul patrulater este numărul de rânduri n înmulțit cu numărul de coloane (n + 1), atunci aranjamentul triunghiular va avea doar jumătate din punctele aranjamentului patrulater.
Aici este ilustrat în figura 2.
- Demo 2
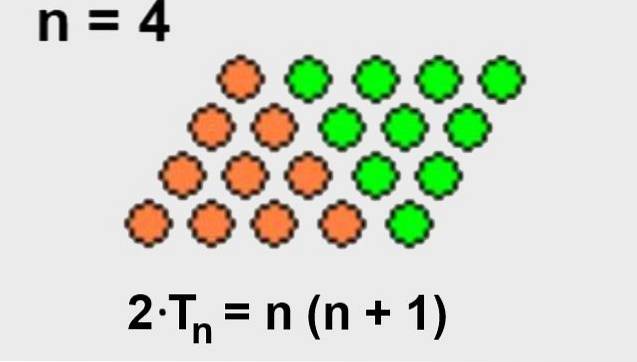
Arată că suma de n-numărul triunghiului cu n-minus unu numărul triunghiular este n pătrat:
Tn + Tn-1= nDouă
S-a arătat deja că numărul triunghiular n-a este dată de:
Tn= ½ n (n + 1)
Prin urmare, numărul triunghiular de mai sus este:
Tn-1 = ½ (n-1) ((n-1) + 1) = ½ n (n - 1)
Suma ambelor este:
Tn + Tn-1 = ½ n (n + 1) + ½ n (n - 1)
Factorul comun ½ n este luat pentru a obține:
Tn + Tn-1 = ½ n [(n + 1) + (n - 1)] = ½ n [n + 1 + n - 1]
Și imediat expresia din paranteză este simplificată:
Tn + Tn-1 = ½ n [2 n] = ½ 2 n ⋅ n
Acum, amintindu-ne că ½ ori 2 este 1 și că n ori n este n pătrat, avem:
Tn + Tn-1 = nDouă
Această proprietate poate fi demonstrată și sub formă geometrică, pur și simplu completați triunghiul pentru a forma un pătrat, așa cum se arată în figura 3.
- Demo 3
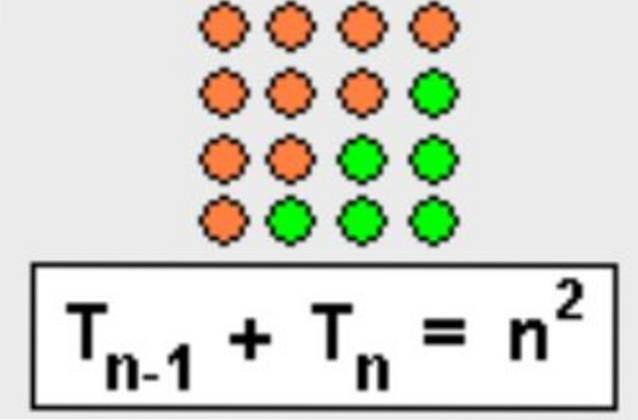
Diferența numărului de ordine triunghiulară n minus numărul de ordine triunghiulară n-1 este n:
Tn - Tn-1 = n
Acest lucru poate fi dovedit pur și simplu reținând că următorul număr triunghiular este obținut din cel precedent folosind formula:
Tn = Tn-1 + n
Și de acolo este evident că Tn - Tn-1 = n. De asemenea, este ușor să-l vizualizați grafic, așa cum se arată în figura 4.
- Demo 5
Suma primelor n numere triunghiulare Sn este egal cu o șesime din produsul lui n înmulțit cu (n + 1) și înmulțit cu (n + 2):
Sn = ⅙ n (n + 1) (n + 2)
Să folosim numărul triunghiular de ordine n: Tn= ½ n (n + 1). Suma primului n numerele triunghiulare o denotă prin Sn
De exemplu, S1 înseamnă suma primului număr triunghiular, care va fi, fără îndoială, 1.
Apoi, să vedem dacă formula pe care încercăm să o testăm este adevărată pentru n = 1:
S1 = ⅙ 1⋅2⋅3 = 1
Într-adevăr, se verifică formula pentru n = 1. Este ușor de vizualizat că suma primelor n + 1 numere triunghiulare va fi suma primului n plus următorul număr triunghiular:
Sn + 1 = Sn + Tn + 1
Acum presupunem că formula pentru Sn este adevărat pentru n, apoi îl substituim în expresia anterioară și adăugăm numărul triunghiular de ordine n + 1:
Sn + 1 = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]
Să vedem pas cu pas ce obțineți:
-Realizăm suma celor două expresii fracționate:
Sn + 1 = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] / 12
-Se ia de la factorul comun al numărătorului la 2 (n + 1) (n + 2) și simplifică:
Sn + 1 = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6
Rezultatul de mai sus este de acord cu formula pentru Sn dacă n este înlocuit cu n + 1, care a fost arătat prin inducție formula pentru suma primilor n termeni triunghiulari.
Număr tetraedric
Rezultatul astfel obținut se numește număr tetraedric de ordinul n, deoarece este ca acumularea straturilor triunghiulare care formează un tetraedru, așa cum se arată în animația următoare.

Referințe
- Camacho J. O apariție neașteptată a numerelor triunghiulare. Recuperat de pe: masscience.com
- Claudio. Numere triunghiulare. Recuperat de la: pur și simplu numere. blogspot. com
- Wikipedia. Număr triunghiular. Recuperat de pe: es.wikipedia.com
- Wikipedia. Număr triunghiular. Recuperat de pe: en.wikipedia.com
- Wikipedia. Număr tretraedric. Recuperat de pe: en.wikipedia.com



Nimeni nu a comentat acest articol încă.