Ce tipuri de integrale există?

tipuri de integrale pe care le găsim în calcul sunt integralele nedeterminate și integralele definite. Deși integralele definite au mult mai multe aplicații decât integralele nedeterminate, este necesar mai întâi să învățăm cum să rezolvăm integralele nedeterminate..

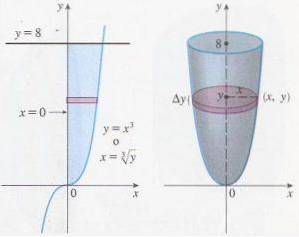
Una dintre cele mai atractive aplicații ale integralelor definite este calcularea volumului unui solid de revoluție. Ambele tipuri de integrale au aceleași proprietăți de liniaritate și, de asemenea, tehnicile de integrare nu depind de tipul integralei.

Dar, în ciuda faptului că este foarte asemănător, există o diferență principală; în primul tip de integral rezultatul este o funcție (care nu este specifică) în timp ce în cel de-al doilea tip rezultatul este un număr.

Tipuri de bază de integrale

Lumea integralelor este foarte largă, dar în cadrul său putem distinge două tipuri de bază de integrale, care au o mare aplicabilitate în viața de zi cu zi..

1- Integrale nedeterminate

Dacă F '(x) = f (x) pentru toate x din domeniul lui f, spunem că F (x) este un antiderivativ, o primitivă sau o integrală a lui f (x).

Pe de altă parte, să observăm că (F (x) + C) '= F' (x) = f (x), ceea ce implică faptul că integrala unei funcții nu este unică, dat fiind că oferă valori diferite constantă C vom obține diferite antiderivative.

Din acest motiv F (x) + C se numește integral nedefinit al lui f (x) și C se numește constanta integrării și o scriem după cum urmează

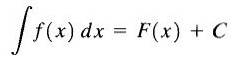
După cum putem vedea, integralul nedefinit al funcției f (x) este o familie de funcții.

De exemplu, dacă doriți să calculați integralul nedefinit al funcției f (x) = 3x², trebuie mai întâi să găsiți un antiderivativ pentru f (x).

Este ușor de văzut că F (x) = x³ este un antiderivativ, deoarece F '(x) = 3x². Prin urmare, se poate concluziona că

∫f (x) dx = ∫3x²dx = x³ + C.

2- Integrale definite

Fie y = f (x) o funcție reală și continuă pe un interval închis [a, b] și F (x) să fie un antiderivativ al lui f (x). Integrala definită a lui f (x) între limitele a și b se numește numărul F (b) -F (a) și se notează după cum urmează

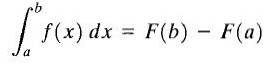
Formula prezentată mai sus este mai bine cunoscută sub numele de „Teorema fundamentală a calculului”. Aici „a” se numește limita inferioară și „b” se numește limita superioară. După cum puteți vedea, integralul definit al unei funcții este un număr.

În acest caz, dacă calculăm integralul definit al lui f (x) = 3x² în intervalul [0,3], vom obține un număr.

Pentru a determina acest număr, alegem F (x) = x³ ca antiderivativ al lui f (x) = 3x². Apoi, calculăm F (3) -F (0) care ne dă rezultatul 27-0 = 27. În concluzie, integralul definit al lui f (x) pe intervalul [0,3] este 27.

Se poate observa că dacă se alege G (x) = x³ + 3, atunci G (x) este un antiderivativ al lui f (x) diferit de F (x), dar acest lucru nu afectează rezultatul din moment ce G (3) - G (0) = (27 + 3) - (3) = 27. Din acest motiv, în integralele definite nu apare constanta integrării.

Una dintre cele mai utile aplicații ale acestui tip de integrală este aceea că permite calcularea ariei (volumului) unei figuri plane (a unui solid de revoluție), stabilind funcții adecvate și limite de integrare (și o axă de rotație).

În cadrul integralelor definite putem găsi diverse extensii ale acestuia, cum ar fi integrale de linie, integrale de suprafață, integrale necorespunzătoare, integrale multiple, printre altele, toate cu aplicații foarte utile în știință și inginerie..

Referințe

1. Casteleiro, J. M. (2012). Este ușor de integrat? Manual de auto-studiu. Madrid: ESIC.
2. Casteleiro, J. M. și Gómez-Álvarez, R. P. (2002). Calcul integral (Ed. Ilustrată). Madrid: Editorial ESIC.
3. Fleming, W. și Varberg, D. E. (1989). Precalcul Matematică. Prentice Hall PTR.
4. Fleming, W. și Varberg, D. E. (1989). Matematica Precalcul: o abordare de rezolvare a problemelor (2, Ed. Ilustrată). Michigan: Prentice Hall.
5. Kishan, H. (2005). Calcul integral. Editori și distribuitori din Atlantic.
6. Purcell, E. J., Varberg, D. și Rigdon, S. E. (2007). Calcul (Ediția a noua). Prentice hall.