linii oblice Acestea sunt cele care sunt înclinate, fie cu privire la o suprafață plană, fie la o altă dreaptă care indică o anumită direcție. De exemplu, luați în considerare cele trei linii trasate într-un plan care apar în figura următoare.
Știm pozițiile lor relative respective, deoarece le comparăm cu o linie de referință, care este de obicei Axa X. denotând orizontală.
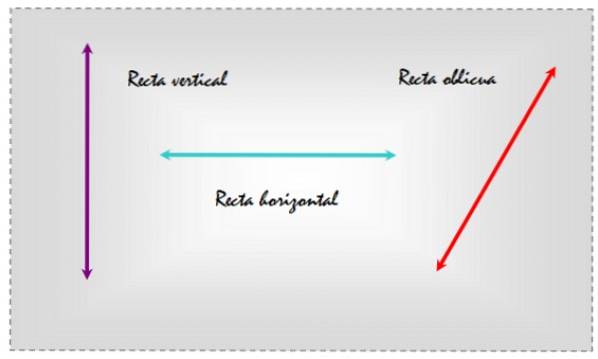
În acest fel, alegând orizontală ca referință, linia din stânga este verticală, cea din centru este orizontală și cea din dreapta este oblică, deoarece este înclinată față de liniile de referință de zi cu zi..
Acum, liniile care se află pe același plan, cum ar fi suprafața hârtiei sau a ecranului, ocupă diferite poziții relative reciproc, în funcție de intersecția sau nu. În primul caz sunt linii secante, în timp ce în al doilea sunt paralele.
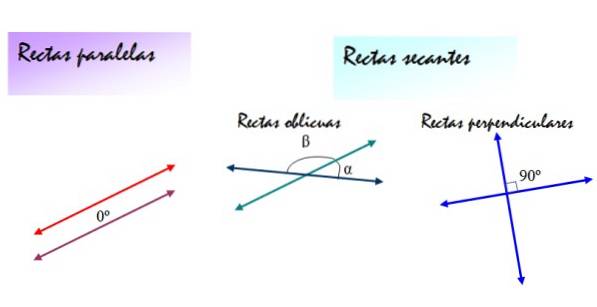
Pe de altă parte, liniile secante pot fi linii oblice sau linii perpendiculare. În ambele cazuri, pantele liniilor sunt diferite, dar liniile oblice formează unghiuri α și β între ele, diferite de 90º, în timp ce unghiurile determinate de liniile perpendiculare sunt întotdeauna de 90º..
Următoarea figură rezumă aceste definiții:
Indice articol
Pentru a cunoaște pozițiile relative ale liniilor în plan, este necesar să cunoaștem unghiul pe care îl formează între ele. Rețineți că liniile sunt:
Paralel: dacă au aceeași pantă (aceeași direcție) și nu se intersectează niciodată, prin urmare punctele lor sunt echidistante.
Coincidenta: atunci când toate punctele sale coincid și, prin urmare, au aceeași pantă, dar distanța dintre punctele sale este zero.
Uscare: dacă pantele lor sunt diferite, distanța dintre punctele lor variază și intersecția este un singur punct.
Deci, o modalitate de a ști dacă două linii din plan sunt secante sau paralele este prin panta lor. Criteriile paralelismului și perpendicularității liniilor sunt următoarele:
Fie L două linii1 și euDouă aparținând unui plan, ale cărui pante sunt respectiv m1 si mDouă. Aceste linii sunt paralele dacă m1 = mDouă și sunt perpendiculare când m1= -1 / mDouă
Dacă, cunoscând pantele a două linii din plan, niciunul dintre criteriile anterioare nu este îndeplinit, vom concluziona că liniile sunt oblice. Cunoscând două puncte ale unei linii, panta este calculată imediat, așa cum vom vedea în secțiunea următoare.
Este posibil să aflăm dacă două linii sunt secante sau paralele găsind intersecția lor, rezolvând sistemul de ecuații pe care le formează: dacă există o soluție sunt secante, dacă nu există o soluție sunt paralele, dar dacă soluțiile sunt infinit, liniile sunt coincidente.
Cu toate acestea, acest criteriu nu ne informează despre unghiul dintre aceste linii, chiar dacă acestea se intersectează.
Pentru a cunoaște unghiul dintre linii, sunt necesari doi vectori sau Da v care aparțin fiecăruia dintre ei. Astfel, este posibil să se cunoască unghiul pe care îl formează prin intermediul produsului scalar al vectorilor, definit în acest fel:
sau•v =u.v.cos α
O linie în plan cartezian poate fi reprezentată în mai multe moduri, cum ar fi:
-Forma de interceptare a pantei: da m este panta liniei și b este intersecția liniei cu axa verticală, ecuația liniei este y = mx + b.
-Ecuație generală pentru o linie dreaptă: Ax + By + C = 0, Unde m = A / B este panta.
În plan cartezian, liniile verticale și orizontale sunt cazuri particulare ale ecuației liniei.
-Liniile verticale: x = a
-Liniile orizontale: y = k
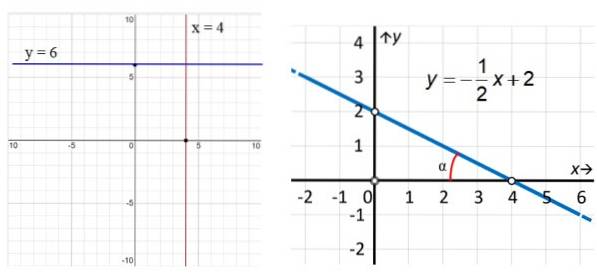
În exemplele din figura 3, linia roșie verticală are ecuația x = 4, în timp ce linia paralelă cu axa x (albastră) are ecuația y = 6. În ceea ce privește linia din dreapta, vedem că este oblică și la pentru a găsi ecuația, folosim punctele evidențiate în figură: (0,2) și (4,0) în acest fel:
m = (șiDouă - Da1) / (XDouă - X1) = (2 - 0) / (0 - 4) = - ½
Tăierea acestei linii cu axa verticală este y = 2, după cum se poate observa din grafic. Cu aceste informații:
y = (-½) x + 2
Determinarea unghiului de înclinare în raport cu axa X este ușoară. Simt că:
α = arctg (2/4) = 26,6º
Prin urmare, unghiul pozitiv de la axa x la linie este: 180º - 26,6º = 153,4º
Liniile oblice apar în multe locuri, este o chestiune de atenție pentru a le găsi în arhitectură, sport, cabluri de alimentare electrică, conducte și multe alte locuri. În natură, sunt prezente și linii oblice, așa cum vom vedea mai jos:
Lumina soarelui călătorește în linie dreaptă, dar forma rotunjită a Pământului afectează modul în care lumina soarelui lovește suprafața..
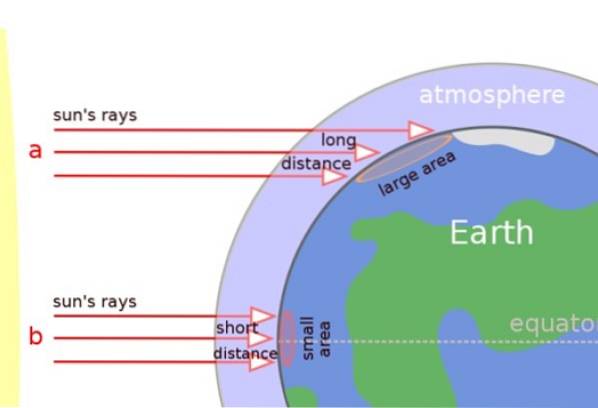
În imaginea de mai jos putem vedea clar că razele soarelui lovesc perpendicular în regiunile tropicale, dar în schimb ajung oblic la suprafață în regiunile temperate și la poli..
Acesta este motivul pentru care razele soarelui parcurg o distanță mai mare prin atmosferă și căldura este răspândită pe o suprafață mai mare (vezi figura). Rezultatul este că zonele din apropierea polilor sunt mai reci.
Când două linii nu sunt în același plan, ele pot fi în continuare oblică sau Incovoiat, precum sunt cunoscute și ele. În acest caz, vectorii lor directori nu sunt paraleli, dar din moment ce nu aparțin aceluiași plan, aceste linii nu se intersectează.
De exemplu, liniile din figura 6 din dreapta sunt clar pe diferite planuri. Dacă îi priviți de sus, puteți vedea că într-adevăr se intersectează, dar nu au un punct în comun. În dreapta vedem roțile bicicletei, ale căror spițe par să se încrucișeze atunci când sunt privite din față.
Nimeni nu a comentat acest articol încă.