scădere vectorială sau scădere vectorială între vectori sau Da v notat cu sau - v, se calculează prin adăugarea vectorului sau cu vectorul opus v. Algebric, scăderea se exprimă după cum urmează:
sau - v = sau + (-v)
Este posibil să se efectueze scăderea vectorului urmând diverse proceduri, de exemplu grafic, în acest fel un vector v este trasat de un segment de linie orientat - o săgeată-.
Lungimea săgeții corespunde modulului vectorului, înclinația - în raport cu o linie de referință dată - indică direcția, iar sfârșitul indică direcția vectorului.
Vectorul opus v are aceeași lungime și direcție, dar direcția opusă. Apoi, înainte de a face scăderea între sau Da v, este necesar să se deseneze vectorul opus v, și adăugați acest vector la u.
Este foarte important să rețineți că scăderea vectorilor nu este comutativă, adică ordinea vectorilor modifică rezultatul, prin urmare:
sau - v ≠ v - sau
Procedura grafică poate fi realizată folosind oricare dintre aceste metode, ale căror etape le vom explica mai jos:
-Metoda triunghiului.
-Metoda paralelogramelor.
Indice articol
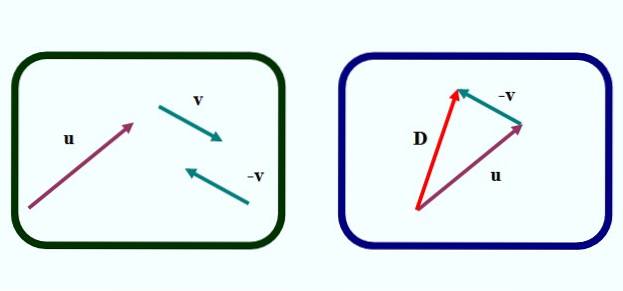
În figura 1 avem prima dintre metode pentru a scădea grafic doi vectori. Este despre metoda triunghiului, deoarece figura care se formează prin stabilirea vectorilor este un triunghi, așa cum putem vedea în imaginea din stânga.
Pentru a face scăderea sau - v procedăm după cum urmează:
-Desenați vectorul -v din vector v, prin traducere cu o riglă și pătrat, dar schimbând direcția săgeții (imaginea din stânga).
-Trece la vector -v în așa fel încât originea sa să coincidă cu sfârșitul vectorului sau (imagine dreapta).
-Apoi este desenat un vector (în roșu în imaginea din dreapta) care merge de la originea lui sau până la sfârșitul anului v. Apel D y este vectorul diferenței:
D = sau - v
În metoda paralelogramului, vectorii de adăugat sau scăzut trebuie să coincidă la punctele lor de origine. Să presupunem că vrem să găsim sau - v Cu vectorii noștri arătați mai sus, pașii pentru a găsi scăderea vectorilor prin această metodă sunt după cum urmează:
-Determinați vectorul opus v, Ce este -v, așa cum este descris mai sus pentru metoda triunghiului.
-Traduceți cu atenție vectori sau Da -v în așa fel încât originile lor să coincidă.
-Acum sunt trasate linii paralele segmentate începând de la capetele fiecărui vector. Figura care se formează este un paralelogram și în cazuri speciale în care vectorii sunt perpendiculari, rezultă un dreptunghi sau un pătrat..
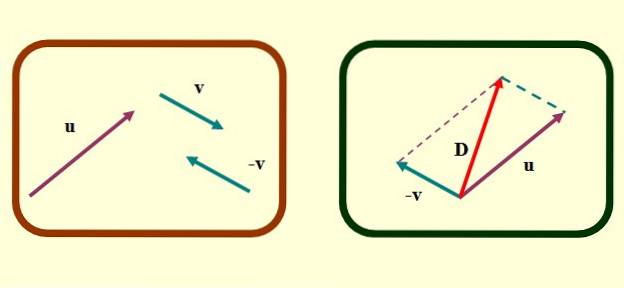
-În cele din urmă, este desenat un vector care începe de la originea comună a sau Da v spre extremă unde se intersectează liniile paralele segmentate. Acesta este vectorul D sau scădere.
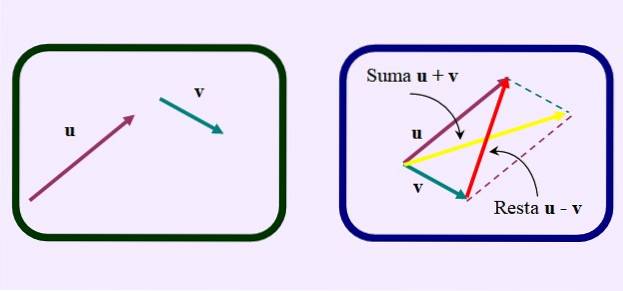
O altă modalitate de a face scăderea este de a desena paralelogramul ca și cum ați dori să adăugați vectorii.
Dar, în loc să deseneze diagonala obișnuită a sumei, care merge de la originea comună la intersecția paralelelor, diagonală opusă sau mai scurtă, așa cum se vede în figură:
O navă navighează pe un râu și o face în direcția opusă curentului. Un observator de pe uscat observă că viteza bărcii este redusă datorită acțiunii curentului.
Viteza este un vector și în acest exemplu, viteza bărcii este îndreptată într-o direcție, iar viteza curentului are aceeași direcție și direcție opusă. Viteza netă a navei este suma ambilor vectori.
De exemplu, dacă instrumentele bărcii indică faptul că se deplasează la v '= + 40 km / h și un observator de pe mal măsoară că barca se deplasează la v = + 30 km / h. Deoarece v = v '+ Vc, unde Vc este viteza curentului care se calculează scăzând viteza v și respectiv v': Vc = v - v '= 30 km / h - 40 km / h = -10 km / h.
În cinematică avem vectori importanți care descriu schimbări:
-Offset pentru schimbări de poziție.
-Viteza medie, pentru a cuantifica cât de rapid variază poziția în timp.
-Accelerare, pentru schimbări de viteză în funcție de timp.
Vectorul de deplasare descrie schimbarea de poziție pe care o experimentează un corp în timpul mișcării sale.
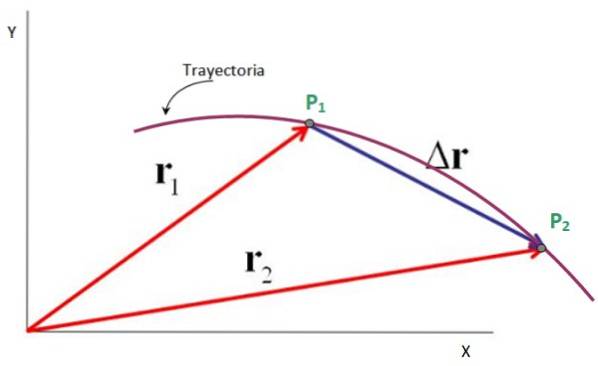
Să vedem, de exemplu, o particulă care descrie calea plană prezentată în figură, în care trece din punctul P1 la punctul PDouă.
Vectorii direcționați de la originea sistemului de coordonate x-y către aceste puncte sunt vectorii de poziție r1 Da rDouă, în timp ce vectorul de deplasare este Δr, care merge de la P1 la PDouă. Este adevarat ca:
Δr = rDouă - r1
Prin urmare, vectorul de deplasare este scăderea dintre vectorul de poziție finală și vectorul de poziție inițială, așa cum se arată în figura următoare. Unitățile sale sunt, de asemenea, cele de poziție: metri, picioare, mile, centimetri și multe altele..
La rândul său, vectorul vitezei medii vm este definit ca compensarea înmulțită cu inversul intervalului de timp:
O particulă care descrie un cerc durează 5 s pentru a trece din punctul A în punctul B. La A are o viteză vLA = 60 km / h spre axa + x și la B este vB = 60 km / h spre + y. Determinați accelerarea medie a acesteia grafic și analitic.
În formă grafică, direcția și direcția accelerației medii sunt determinate de:
În imaginea următoare este scăderea vB - vLA, folosind metoda triunghiului, deoarece accelerarea medie lam este proporțional cu Δv. Triunghiul format are cele două picioare egale și, prin urmare, unghiurile interne acute măsoară 45º fiecare..
Analitic, dacă direcția + x coincide cu vectorul unitar eu și direcția + y cu vectorul unitar j, atunci:
Δv = 60 km / h j - 60 km / h eu
Luând Δt = 5 s, conform informațiilor din enunț, accelerația medie este:
lam = (60 km / h j - 60 km / h i) / 5 s = 12 (j-eu) km / (h.s)
Nimeni nu a comentat acest articol încă.