Exemple și exerciții din seria Power

A serie de puteri constă într-o însumare a termenilor sub forma puterilor variabilei X, sau mai general, de x-c, Unde c este un număr real constant. În notație de însumare, o serie de puteri este exprimată după cum urmează:

∑a_n (x -c)ⁿ = a_sau + la₁ (x - c) + a_Două (x - c)^Două + la₃ (x - c)³ +… + A_n (x - c)ⁿ

Unde coeficienții a_sau, la₁, la_Două… Sunt numere reale și seria începe de la n = 0.

Această serie este axată pe valoare c care este constant, dar puteți alege care c este egal cu 0, caz în care seria de putere se simplifică la:

∑a_n Xⁿ = a_sau + la₁ x + a_Două X^Două + la₃ X³ +… + A_n Xⁿ

Seria începe cu la_sau(x-c)⁰ Da la_sauX⁰ respectiv. Dar știm că:

(x-c)⁰= x⁰ = 1

Prin urmare la_sau(x-c)⁰ = la_sauX⁰ = la_sau (termen independent)

Lucrul bun despre seria Power este că puteți exprima funcții cu ele și acest lucru are multe avantaje, mai ales dacă doriți să lucrați cu o funcție complicată.

Atunci când este cazul, în loc să se utilizeze direct funcția, se folosește extinderea sa în seria de putere, care poate fi mai ușor de derivat, integrat sau lucrat numeric..

Desigur, totul este condiționat de convergența seriei. O serie converge atunci când adăugarea unui anumit număr mare de termeni dă o valoare fixă. Și dacă adăugăm încă mai mulți termeni, continuăm să obținem acea valoare.

Indice articol

• 1 Funcționează ca serie Power
  • 1.1 Seria de puteri geometrice
• 2 Cum se găsește expansiunea în serie a puterilor unei funcții
• 3 Exercițiu
  • 3.1 - Exercițiu rezolvat 1
  • 3.2 - Exercițiu rezolvat 2
• 4 Referințe

Funcționează ca serie Power

Ca exemplu de funcție exprimată ca serie de putere, să luăm f (x) = e^X.

Această funcție poate fi exprimată în termeni de o serie de puteri după cum urmează:

și^X  ≈ 1 + x + (x^Două / 2!) + (X³ / 3!) + (X⁴ / 4!) + (X⁵ / 5!) + ...

Unde! = n. (n-1). (n-2). (n-3) ... și este nevoie de 0! = 1.

Vom verifica cu ajutorul unui calculator că într-adevăr seria coincide cu funcția dată în mod explicit. De exemplu, să începem prin a face x = 0.

Știm că e⁰ = 1. Să vedem ce face seria:

și⁰ ≈ 1 + 0 + (0^Două / 2!) + (0³ / 3!) + (0⁴ / 4!) + (0⁵ / 5!) + ... = 1

Și acum să încercăm cu x = 1. Un calculator arată asta și¹ = 2,71828, și apoi să comparăm cu seria:

și¹ ≈ 1 + 1 + (1^Două / 2!) + (1³ / 3!) + (1⁴ / 4!) + (1⁵ / 5!) +… = 2 + 0,5000 + 0,1667 + 0,0417 + 0,0083 +… ≈ 2,7167

Cu doar 5 termeni avem deja o potrivire exactă e ≈ 2,71. Seria noastră are încă puțin de parcurs, dar pe măsură ce se adaugă mai mulți termeni, seria converge cu siguranță la valoarea exactă a și. Reprezentarea este exactă când n → ∞.

Dacă analiza de mai sus se repetă la n = 2 se obțin rezultate foarte similare.

În acest fel suntem siguri că funcția exponențială f (x) = e^X poate fi reprezentat de această serie de puteri:

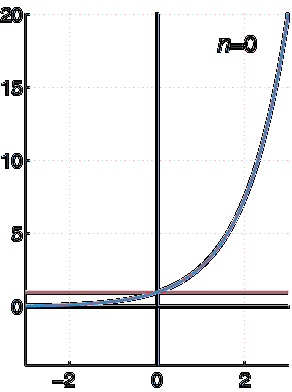
Seria geometrică de puteri

Functia f (x) = e^X nu este singura funcție care acceptă o reprezentare în serie de putere. De exemplu, funcția  F(x) = 1/1 - x  seamănă mult cu binecunoscutul serii geometrice convergente:

∑a.rⁿ = a / 1 - r

Este suficient să faceți a = 1 și r = x pentru a obține o serie potrivită pentru această funcție, care este centrată la c = 0:

Cu toate acestea, se știe că această serie este convergentă pentru │r│<1, por lo tanto la representación es válida únicamente en el intervalo (-1,1), aunque la función sea válida para todo x, excepto x=1.

Când doriți să definiți această funcție într-un alt interval, vă concentrați pur și simplu pe o valoare adecvată și ați terminat..

Cum se găsește extinderea în serie a puterilor unei funcții

Orice funcție poate fi dezvoltată într-o serie de puteri centrată pe c, atâta timp cât are derivate de toate ordinele la x = c. Procedura folosește următoarea teoremă, numită Teorema lui Taylor:

Fie f (x) o funcție cu derivate de ordine n, notat ca F⁽ⁿ⁾, care admite o serie de expansiuni de puteri în interval Eu. Dezvoltarea sa în seria Taylor este:

Astfel încât:

f (x) = f (c) + f '(c) (x-c) + f "(c) (x-c)^Două / 2 + f "(c) (x-c)³ / 6 + ... R_n

Unde R_n, care este al n-lea termen al seriei, se numește reziduu:

Când c = 0 se numește seria Seria Maclaurin.

Această serie dată aici este identică cu seria dată la început, doar că acum avem o modalitate de a găsi în mod explicit coeficienții fiecărui termen, dat de:

Cu toate acestea, trebuie să ne asigurăm că seria converge la funcția care trebuie reprezentată. Se întâmplă că nu fiecare serie Taylor converge în mod necesar la f (x) care a fost avut în vedere la calcularea coeficienților la_n.

Acest lucru se întâmplă deoarece probabil derivatele funcției, evaluate în x = c coincid cu aceeași valoare a derivatelor alteia, de asemenea în x = c. În acest caz, coeficienții ar fi aceiași, dar dezvoltarea ar fi ambiguă, deoarece nu este sigur cărei funcții îi corespunde..

Din fericire există o modalitate de a ști:

Criteriul convergenței

Pentru a evita ambiguitatea, dacă R_n → 0 când n → ∞ pentru toate x din intervalul I, seria converge la f (x).

Exercițiu

- Exercițiu rezolvat 1

Găsiți seria de putere geometrică pentru funcție f (x) = 1/2 - x centrat la c = 0.

Soluţie

Funcția dată trebuie exprimată în așa fel încât să coincidă cât mai aproape cu 1 / 1- x, a cărei serie este cunoscută. Prin urmare, să rescriem numărătorul și numitorul, fără a modifica expresia originală:

1/2 - x = (1/2) / [1 - (x / 2)]

Deoarece ½ este constant, acesta iese din însumare și este scris în termenii noii variabile x / 2:

Rețineți că x = 2 nu aparține domeniului funcției și conform criteriului de convergență dat în secțiune Seria de puteri geometrice, extinderea este valabilă pentru │x / 2│< 1 o equivalentemente -2 < x < 2.

- Exercițiu rezolvat 2

Găsiți primii 5 termeni ai expansiunii din seria Maclaurin a funcției f (x) = sin x.

Soluţie

Pasul 1

Derivatele se găsesc mai întâi:

-Derivată de ordinul 0: este aceeași funcție f (x) = sin x

-Prima derivată: (sin x) '= cos x

-A doua derivată: (sin x) "= (cos x) '= - sin x

-A treia derivată: (sin x) "= (-sen x) '= - cos x

-A patra derivată: (sin x) "= (- cos x) '= sin x

Pasul 2

Apoi fiecare derivat este evaluat la x = c, la fel ca o expansiune Maclaurin, c = 0:

sin 0 = 0; cos 0 = 1; - sin 0 = 0; -cos 0 = -1; sin 0 = 0

Pasul 3

Coeficienții a sunt construiți_n;

la_sau = 0/0! = 0; la₁ = 1/1! = 1; la_Două = 0/2! = 0; la₃ = -1 / 3!; la₄ = 0/4! = 0

Pasul 4

În cele din urmă, seria este asamblată în funcție de:

sin x ≈ 0.x⁰ + 1. x¹ + 0 .x^Două - (1/3!) X³ + 0.x⁴… = X - (1/3!)) X³  +...

Cititorul are nevoie de mai mulți termeni? Câte mai multe, seria se apropie de funcție.

Rețineți că există un model în coeficienți, următorul termen diferit de zero este a₅ și toți cei cu indice impar sunt, de asemenea, diferiți de 0, alternând semnele, astfel încât:

sin x ≈ x - (1/3!)) x³  + (1/5!)) X⁵ - (1/7!)) X⁷  +... .

Este lăsat ca exercițiu pentru a verifica dacă converge, puteți utiliza criteriul coeficientului pentru convergența seriilor.

Referințe

1. Fundația CK-12. Power Series: reprezentarea funcțiilor și operațiilor. Recuperat de pe: ck12.org.
2. Engler, A. 2019. Calcul integral. Universitatea Națională a Litoralului.
3. Larson, R. 2010. Calculul unei variabile. 9. Ediție. Dealul Mcgraw.
4. Texte gratuite de matematică. Serie de puteri. Recuperat de pe: math.liibretexts.org.
5. Wikipedia. Serie de puteri. Recuperat de pe: es.wikipedia.org.