Istoricul sistemului octal, sistemul de numerotare, conversiile

sistem octal este un sistem de numerotare pozițională bazat pe opt (8); adică este format din opt cifre, care sunt: ​​0, 1, 2, 3, 4, 5, 6 și 7. Prin urmare, fiecare cifră a unui număr octal poate avea orice valoare de la 0 la 7. Numerele octale sunt formate din numere binare.

Acest lucru se întâmplă deoarece baza sa este o putere exactă de două (2). Adică numerele care aparțin sistemului octal se formează atunci când sunt grupate în trei cifre consecutive, ordonate de la dreapta la stânga, obținându-se astfel valoarea zecimală a acestora..

Indice articol

• 1 Istorie
• 2 Sistem de numerotare octală
• 3 Conversia de la octal la sistem zecimal
  • 3.1 Exemplul 1
  • 3.2 Exemplul 2
• 4 Conversia din sistem zecimal în octal
  • 4.1 Exemplu
• 5 Conversia de la octal la sistem binar
• 6 Conversia din sistem binar în octal
• 7 Conversia de la octal la hexazecimal și invers
  • 7.1 Exemplu
• 8 Referințe

Poveste

Sistemul octal își are originea în cele mai vechi timpuri, când oamenii își foloseau mâinile pentru a număra animalele de la opt la opt.

De exemplu, pentru a număra numărul vacilor dintr-un grajd, a început să se numere cu mâna dreaptă, unind degetul mare cu degetul mic; apoi pentru a număra al doilea animal, degetul mare a fost unit cu degetul arătător și așa mai departe cu degetele rămase ale fiecărei mâini, până la finalizarea 8.

Există posibilitatea ca în timpuri străvechi sistemul de numerotare octal să fie folosit înainte de zecimal pentru a putea număra spații interdigitale; adică numără toate degetele, cu excepția degetelor mari.

Ulterior a fost stabilit sistemul de numerotare octal, care a provenit din sistemul binar, deoarece are nevoie de multe cifre pentru a reprezenta doar un număr; de atunci au fost create sistemele octal și hexagonal, care nu necesită atât de multe cifre și pot fi ușor convertite în sistemul binar.

Sistem de numerotare octal

Sistemul octal este format din opt cifre care merg de la 0 la 7. Acestea au aceeași valoare ca și în cazul sistemului zecimal, dar valoarea lor relativă se modifică în funcție de poziția pe care o ocupă. Valoarea fiecărei poziții este dată de puterile bazei 8.

Pozițiile cifrelor dintr-un număr octal au următoarele greutăți:

8⁴, 8³, 8^Două, 8¹, 8⁰, punctul octal, 8^-1, 8^-Două, 8^-3, 8^-4, 8^-5.

Cea mai mare cifră octală este 7; în acest fel, când se numără în acest sistem, o poziție a unei cifre este mărită de la 0 la 7. Când este atins 7, acesta este reciclat la 0 pentru următorul număr; în acest fel se crește poziția următoarei cifre. De exemplu, pentru a număra secvențe, în sistemul octal va fi:

• 0, 1, 2, 3, 4, 5, 6, 7, 10.
• 53, 54, 55, 56, 57, 60.
• 375, 376, 377, 400.

Există o teoremă fundamentală care se aplică sistemului octal și este exprimată după cum urmează:

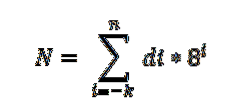
În această expresie di reprezintă cifra înmulțită cu puterea bazei 8, care indică valoarea locului fiecărei cifre, în același mod în care este ordonată în sistemul zecimal..

De exemplu, aveți numărul 543.2. Pentru a-l duce la sistemul octal, se descompune după cum urmează:

N = ∑ [(5 _* 8^Două) + (4 _* 8¹) + (3 _*8⁰) + (2 _*8^-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0,125)

N = 320 +32 + 2 + 0,25 = 354 + 0,25_d

În acest fel trebuie să 543.2_ce = 354,25_d. Indicele q indică faptul că este un număr octal care poate fi reprezentat și de numărul 8; iar indicele d se referă la numărul zecimal, care poate fi reprezentat și de numărul 10.

Conversia de la octal la sistem zecimal

Pentru a converti un număr din sistemul octal la echivalentul său din sistemul zecimal, trebuie doar să multiplicați fiecare cifră octală cu valoarea sa de poziție, începând de la dreapta.

Exemplul 1

732₈ = (7_* 8^Două) + (3_* 8¹) + (2_* 8⁰) = (7 _* 64) + (3 _* 8) + (2 _* 1)

732₈= 448 +24 +2

732₈= 474₁₀

Exemplul 2

26.9₈ = (2 _*8¹) + (6_* 8⁰) + (9_* 8^-1) = (2 _* 8) + (6 _* 1) + (9 _* 0,125)

26.9₈ = 16 + 6 + 1.125

26.9₈= 23.125₁₀

Conversia de la sistemul zecimal la octal

Un număr întreg zecimal poate fi convertit într-un număr octal folosind metoda împărțirii repetate, în care numărul întreg zecimal este împărțit la 8 până când coeficientul este egal cu 0, iar resturile fiecărei diviziuni vor reprezenta numărul octal..

Reziduurile sunt comandate de la ultimul la primul; adică primul rest va fi cea mai puțin semnificativă cifră a numărului octal. În acest fel, cea mai semnificativă cifră va fi ultima rămase..

Exemplu

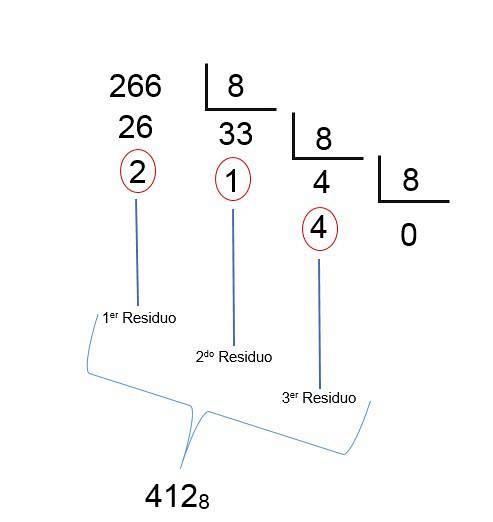
Octala numărului zecimal 266₁₀

- Împarte numărul zecimal 266 la 8 = 266/8 = 33 + restul de 2.

- Apoi împărțiți 33 cu 8 = 33/8 = 4 + restul de 1.

- Împarte 4 la 8 = 4/8 = 0 + restul de 4.

Deoarece cu ultima diviziune se obține un coeficient mai mic de 1, înseamnă că rezultatul a fost găsit; Trebuie doar să ordonați resturile invers, în așa fel încât numărul octal al zecimalei 266 să fie 412, așa cum se poate vedea în următoarea imagine:

Conversia de la octal la sistem binar

Conversia de la octal la binar se face prin convertirea cifrei octale la cifra sa binară echivalentă, formată din trei cifre. Există un tabel care arată cum sunt convertite cele opt cifre posibile:

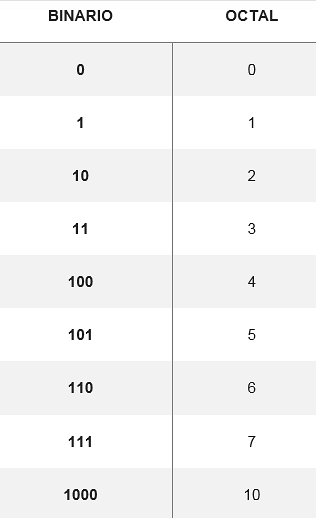
Din aceste conversii puteți schimba orice număr din sistemul octal în binar, de exemplu, pentru a converti numărul 572₈ echivalentele lor sunt căutate în tabel. Astfel, trebuie să:

5₈ = 101

7₈= 111

Două₈ = 10

Prin urmare, 572₈ este echivalent în sistemul binar cu 10111110.

Conversia de la binar la octal

Procesul de conversie a numerelor întregi binare în numere întregi octale este operația inversă a procesului anterior.

Adică, biții numărului binar sunt grupați în două grupuri de trei biți, începând de la dreapta la stânga. Apoi, conversia de la binar la octal se face cu tabelul anterior.

În unele cazuri, numărul binar nu va avea grupuri de 3 biți; pentru a-l completa, se adaugă unul sau două zerouri în stânga primului grup.

De exemplu, pentru a schimba numărul binar 11010110 în octal, procedați în felul următor:

- Se formează grupuri de 3 biți începând din dreapta (ultimul bit):

11010110

- Deoarece primul grup este incomplet, se adaugă un zero din partea de sus:

011010110

- Conversia se face din tabel:

011 = 3

010 = 2

110 = 6

Astfel, numărul binar 011010110 este egal cu 326₈.

Conversia de la octal la hexazecimal și invers

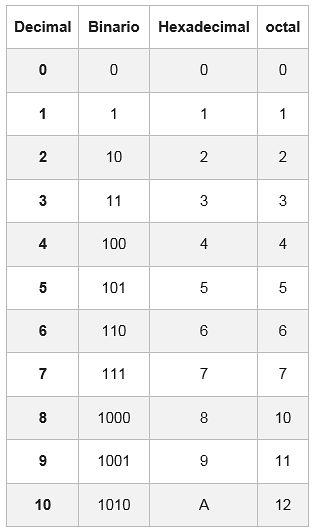
Pentru a trece de la un număr octal la sistemul hexazecimal sau de la hexazecimal la octal, este necesar să convertiți numărul mai întâi în binar, apoi în sistemul dorit.

Pentru aceasta, există un tabel în care fiecare cifră hexazecimală este reprezentată cu echivalentul ei în sistemul binar, compusă din patru cifre.

În unele cazuri, numărul binar nu va avea grupuri de 4 biți; pentru a o completa, se adaugă unul sau două zerouri în stânga primului grup

Exemplu

Conversia numărului octal 1646 în număr hexazecimal:

- Convertiți numărul din octal în binar

1₈ = 1

6₈ = 110

4₈ = 100

6₈ = 110

- Astfel, 1646₈ = 1110100110.

- Pentru a converti de la binar la hexazecimal, acestea sunt mai întâi ordonate într-un grup de 4 biți, începând de la dreapta la stânga:

11 1010 0110

- Primul grup este completat cu zerouri, astfel încât să poată avea 4 biți:

0011 1010 0110

- Conversia se face din sistemul binar în sistemul hexazecimal. Echivalențele sunt substituite prin intermediul tabelului:

0011 = 3

1010 = A

0110 = 6

Astfel, numărul octal 1646 este echivalent cu 3A6 în sistemul hexazecimal..

Referințe

1. Bressan, A. E. (1995). Introducere în sistemele de numerotare. Universitatea de Afaceri din Argentina.
2. Harris, J. N. (1957). Introducere în sistemele de numerotare binare și octale: Lexington, agenția de informații tehnice pentru serviciile armate din Mass.
3. Kumar, A. A. (2016). Bazele circuitelor digitale. Pvt de învățare.
4. Peris, X. C. (2009). Sisteme operative unice.
5. Ronald J. Tocci, N. S. (2003). Sisteme digitale: principii și aplicații. Pearson Education.