
Teorema lui Thévenin în ce constă, aplicații și exemple
Teorema lui Thévenin afirmă că un circuit cu bornele A și B poate fi înlocuit cu unul echivalent format dintr-o sursă și o rezistență de serie, ale cărei valori dau aceeași diferență de potențial între A și B și aceeași impedanță ca circuitul original.
Această teoremă a fost făcută cunoscută în 1883 de inginerul francez Léon Charles Thévenin, dar se susține că a fost enunțată cu treizeci de ani mai devreme de către fizicianul german Hermann von Helmholtz.

Utilitatea sa constă în faptul că, chiar și atunci când circuitul original este complex sau necunoscut, în scopul unei sarcini sau impedanțe plasate între bornele A și B, circuitul echivalent Thévenin simplu se comportă în același mod ca originalul.
Indice articol
- 1 Cum calculați tensiunea echivalentă pas cu pas?
- 1.1 - Experimental
- 1.2 - Rezolvarea circuitului
- 2 Aplicații ale teoremei lui Thévenin (partea I)
- 2.1 Exemplul 1a (calculul tensiunii echivalente pas cu pas)
- 2.2 Exemplul 1b (curent în sarcină utilizând echivalentul Thévenin)
- 3 Dovada teoremei lui Thévenin
- 4 Aplicarea teoremei lui Thévenin (partea II)
- 4.1 Exemplul 2a (rezistență echivalentă Thévenin)
- 4.2 Exemplul 2b
- 4.3 Exemplul 2c
- 5 Aplicarea teoremei lui Thévenin (partea III)
- 5.1 Exemplul 3
- 6 Referințe
Cum calculați tensiunea echivalentă pas cu pas?
Tensiunea sau diferența de potențial a circuitului echivalent pot fi obținute în următoarele moduri:
- Experimental
Obținerea tensiunii Thévenin echivalente
Dacă este un dispozitiv sau echipament care se află într-o „cutie neagră”, diferența de potențial între bornele A și B se măsoară cu un voltmetru sau cu un osciloscop. Este foarte important ca nici o sarcină sau impedanță să nu fie plasată între bornele A și B.
Un voltmetru sau un osciloscop nu reprezintă nicio sarcină pe terminale, deoarece ambele dispozitive au o impedanță foarte mare (în mod ideal infinită) și ar fi ca și cum terminalele A și B ar fi fără sarcină. Tensiunea sau tensiunea obținută în acest mod este tensiunea echivalentă Thévenin.
Obținerea impedanței echivalente Thévenin
Pentru a obține impedanța echivalentă dintr-o măsurare experimentală, o rezistență cunoscută este plasată între bornele A și B, iar căderea de tensiune sau semnalul de tensiune sunt măsurate cu un osciloscop..
Din căderea de tensiune a rezistenței cunoscute dintre borne, se poate obține curentul care curge prin ea.
Produsul curentului obținut cu rezistența echivalentă plus căderea de tensiune măsurată în rezistența cunoscută este egal cu tensiunea Thévenin echivalentă obținută anterior. Din această egalitate se elimină impedanța Thévenin echivalentă.
- Rezolvarea circuitului
Calculul tensiunii echivalente Thévenin
În primul rând, orice sarcină sau impedanță este deconectată de la bornele A și B.
După cum se cunoaște circuitul, se aplică teoria mesh-ului sau legile lui Kirchhoff pentru a găsi tensiunea la terminale. Această tensiune va fi echivalentul lui Thévenin.
Calculul impedanței echivalente Thévenin
Pentru a obține impedanța echivalentă, procedăm la:
- Înlocuiți sursele de tensiune ale circuitului original cu scurtcircuite "impedanță zero" și sursele de curent ale circuitului original cu cele deschise "impedanță infinită".
- Apoi, impedanța echivalentă este calculată urmând regulile impedanțelor de serie și impedanțelor paralele.
Aplicații ale teoremei lui Thévenin (partea I)
Vom aplica teorema lui Thévenin pentru a rezolva unele circuite. În această primă parte considerăm un circuit care are doar surse de tensiune și rezistențe.
Exemplul 1a (calculul stresului echivalent pas cu pas)
Figura 2 prezintă circuitul care se află într-o cutie cerească care are două baterii de forță electromotoare V1 și respectiv V2 și rezistențe R1 și R2, circuitul are bornele A și B în care poate fi conectată o sarcină.
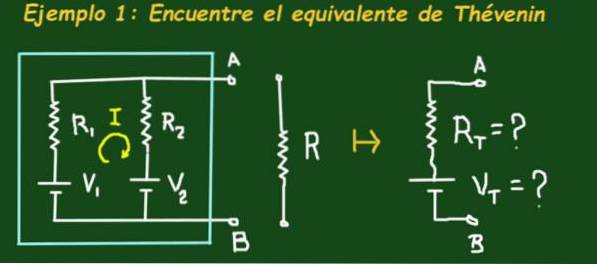
Scopul este de a găsi circuitul echivalent Thévenin, adică de a determina valorile Vt și Rt ale circuitului echivalent. Aplicați următoarele valori: V1 = 4V, V2 = 1V, R1 = 3Ω, R2 = 6Ω și R = 1Ω.
Soluție pas cu pas
Pasul 1
Vom determina tensiunea la bornele A și B atunci când nu este pusă nicio sarcină pe ele.
Pasul 2
Circuitul de rezolvat constă dintr-o singură plasă prin care circulă un curent I pe care l-am luat pozitiv în sensul acelor de ceasornic.
Pasul 3
Trecem prin plasă începând cu colțul din stânga jos. Calea duce la următoarea ecuație:
V1 - I * R1 - I * R2 - V2 = 0
Pasul 4
Rezolvăm curentul de rețea I și obținem:
I = (V1 -V2) / (R1 + R2) = (4V - 1V) / (3Ω + 6Ω) = ⅓ A
Pasul 5
Cu curentul de plasă putem determina diferența de tensiune între A și B, care este:
Vab = V1 - I * R1 = 4V - ⅓ A * 3Ω = 3V
Adică tensiunea echivalentă Thevenin este: Vt = 3V.
Pasul 6 (rezistență echivalentă Thévenin)
Acum procedăm la calcularea rezistenței echivalente Thévenin, pentru care și așa cum am menționat anterior, sursele de tensiune sunt înlocuite cu un cablu.
În acest caz, avem doar două rezistențe în paralel, deci rezistența echivalentă Thévenin este:
Rt = (R1 * R2) / (R1 + R2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω
Exemplul 1b (curent în sarcină utilizând echivalentul Thévenin)
Conectați ca sarcină la bornele A și B o rezistență R = 1Ω la circuitul echivalent și găsiți curentul care curge prin sarcina respectivă.
Soluţie
Când rezistența R este conectată la circuitul echivalent Thevenin, avem un circuit simplu care constă dintr-o sursă Vt o rezistență Rt în serie cu rezistența R.
Vom numi Ic curentul care curge prin sarcina R, astfel încât ecuația mesh să arate astfel:
Vt - Ic * Rt - Ic * R = 0
din care rezultă că Ic este dat de:
Ic = Vt / (Rt + R) = 3V / (2Ω + 1Ω) = 1 A
Dovada teoremei lui Thévenin
Pentru a verifica dacă teorema lui Thévenin se menține, conectați R la circuitul original și găsiți curentul care curge prin R aplicând legea ochiurilor la circuitul rezultat.
Circuitul rezultat rămâne și ecuațiile sale de plasă rămân așa cum se arată în figura următoare:
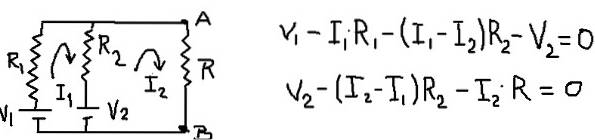
Prin adăugarea ecuațiilor mesh, este posibil să găsim curentul mesh I1 în funcție de curentul I2. Apoi este substituită în a doua ecuație mesh și o ecuație este lăsată cu I2 ca singură necunoscută. Următorul tabel prezintă operațiunile.
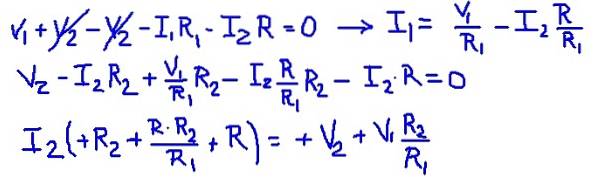
Apoi se substituie valorile rezistenței și tensiunilor surselor, obținându-se valoarea numerică a curentului de plasă I2.

Curentul de plasă I2 este curentul care curge prin rezistența la sarcină R și valoarea găsită de 1 A coincide pe deplin cu cea găsită anterior cu circuitul Thévenin echivalent..
Aplicarea teoremei lui Thévenin (partea II)
În această a doua parte, teorema Thévenin va fi aplicată într-un circuit care are surse de tensiune, sursă de curent și rezistențe.
Exemplul 2a (rezistență echivalentă Thévenin)
Obiectivul este de a determina circuitul echivalent Thévenin corespunzător circuitului din figura următoare, atunci când bornele sunt fără rezistența de 1 ohm, atunci se plasează rezistența și se determină curentul care circulă prin el.
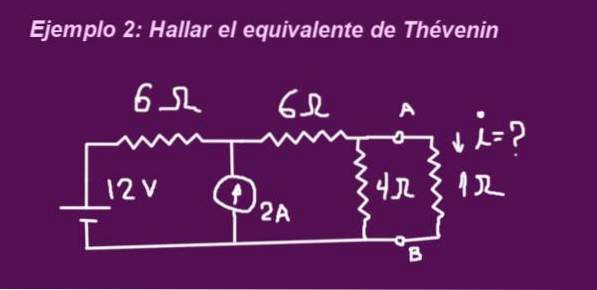
Soluţie
Pentru a găsi rezistența echivalentă, eliminați rezistența la sarcină (în acest caz 1 ohm). De asemenea, sursele de tensiune sunt înlocuite de un scurtcircuit, iar sursele de curent cu un circuit deschis..
În acest fel, circuitul pentru care va fi calculată rezistența echivalentă este cel prezentat mai jos:
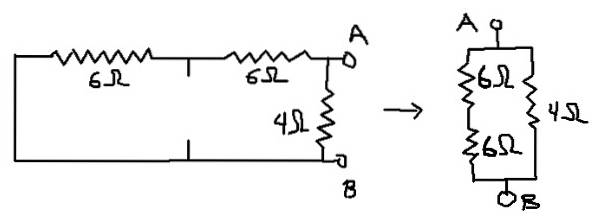
Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω, care este rezistența echivalentă a Thevenin (Rth).
Exemplul 2b
Calculați tensiunea echivalentă Thévenin.
Soluţie
Pentru a calcula tensiunea echivalentă Thévenin luăm în considerare următorul circuit, în care vom plasa curenții în I1 și I2 în ramurile indicate în figura următoare:
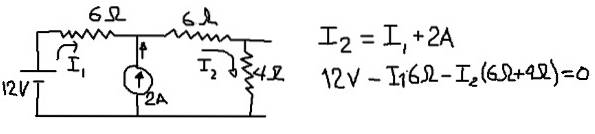
Figura anterioară arată ecuația nodurilor curente și ecuația tensiunilor atunci când este traversată rețeaua externă. Din a doua dintre ecuații curentul I1 este eliminat:
I1 = 2 - I2 * (5/3)
Această ecuație este substituită în ecuația nodurilor:
I2 = 2 - (5/3) I2 + 2 ===> I2 (8/3) = 4 ===> I2 = 12/8 = 1,5 A
Aceasta înseamnă că căderea de tensiune pe rezistorul de 4 ohmi este de 6 volți..
Pe scurt, tensiunea Thévenin este Vth = 6 V..
Exemplul 2c
Găsirea circuitului și curentului echivalent Thevenin în rezistența de încărcare.
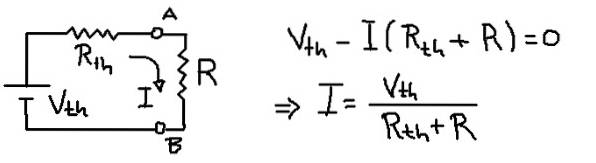
Soluţie
Figura anterioară arată circuitul echivalent Thévenin cu rezistența la sarcină R. Din ecuația tensiunii din plasă, se deduce curentul I care curge prin rezistența la sarcină R.
I = Vth / (Rth + R) = 6V / (3Ω + 1Ω) = 1,5 A
Aplicarea teoremei lui Thévenin (partea III)
În această a treia parte a aplicației teoremei lui Thévenin, se consideră un circuit de curent alternativ care conține o sursă de tensiune alternativă, un condensator, o inductanță și o rezistență..
Exemplul 3
Scopul este de a găsi circuitul Thévenin echivalent cu următorul circuit:
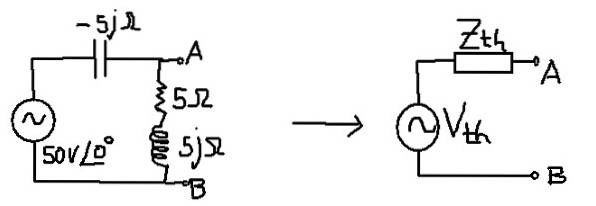
Soluţie
Impedanța echivalentă corespunde cu cea a condensatorului în paralel cu combinația în serie a rezistenței și inductanței.
Inversa impedanței echivalente este dată de:
Zeq ^ -1 = (-5j) ^ - 1 + (5 + 5j) ^ - 1 = (1/5) j + ((1/10 + (1/10) j) = (1/10 + 3 / 10 j) Mho
Și impedanța echivalentă va fi atunci:
Zeq = (1 - 3 j) Ohm
Curentul complex I poate fi derivat din ecuația mesh:
50V∠0 - I (-5 j + 5 + 5j) = 50V∠0 - I * 5 = 0 ===> I = 10A ∠0
Acum se calculează căderea de tensiune a rezistenței plus inductanța, adică tensiunea Vab care va fi tensiunea Thévenin echivalentă:
Vab = I * (5 + 5 j) Ω = 10A ∠0 * 5Ω∠45º = 50V∠45º
Cu alte cuvinte, tensiunea echivalentă are aceeași valoare de vârf a sursei originale, dar este defazată la 45 de grade: Vth = 50V∠45º
Referințe
- Tutoriale electronice, teorema lui Thevenin. Recuperat de la: electronic-tutorials.ws
- Întrebări și răspunsuri despre teoria rețelei. Teorema lui Thevenin. Recuperat de pe: sanfoundry.com
- Teorema lui Thevenin. Procedură pas cu pas. Recuperat de pe: electricaltechnology.org
- Teorema lui Thevenin. Exemplu rezolvat pas cu pas. Recuperat de pe: electricsimple.blogspot.com
- Atelier despre teoremele lui Thevenin și Norton. Recuperat de pe: web.iit.edu
- Wikipedia. Teorema lui Thévenin. Recuperat de pe: wikipedia.com



Nimeni nu a comentat acest articol încă.