
Teorema lui Torricelli în ce constă, formule și exerciții
Teorema lui Torricelli Principiul Torricelli afirmă că viteza lichidului care iese prin orificiul din peretele unui rezervor sau container este identică cu cea a unui obiect căruia i se permite să cadă liber de la o înălțime egală cu cea a suprafeței libere a lichidului până la gaură.
Teorema este ilustrată în următoarea figură:
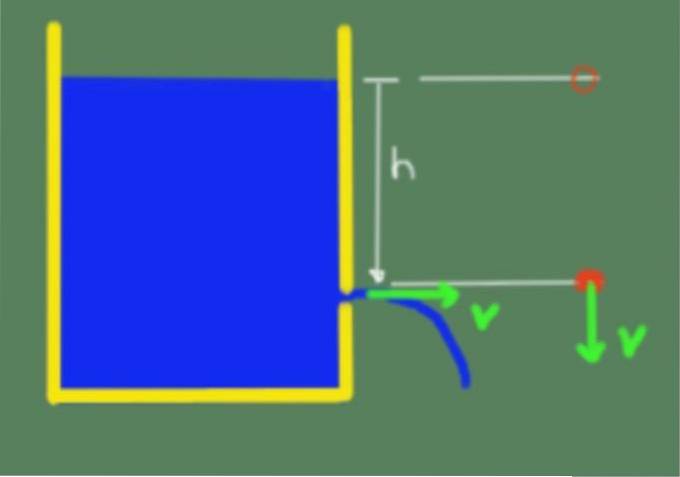
Datorită teoremei lui Torricelli putem afirma că viteza de ieșire a lichidului printr-un orificiu care se află la înălțimea h sub suprafața liberă a lichidului este dată de următoarea formulă:
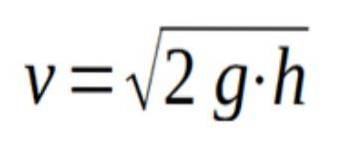
Unde g este accelerația gravitației și h este înălțimea de la gaură la suprafața liberă a lichidului.
Evangelista Torricelli a fost un fizician și matematician născut în orașul Faenza, Italia în 1608. Torricelli este creditat cu invenția barometrului cu mercur și ca recunoaștere există o unitate de presiune numită „torr”, echivalentă cu un milimetru de mercur (mm Hg).
Indice articol
- 1 Dovada teoremei
- 1.1 Obiectul care cade
- 1.2 Lichid care iese din gaură
- 2 exerciții rezolvate
- 2.1 Exercițiul 1
- 3 I) Conducta mică de evacuare a unui rezervor de apă este la 3 m sub suprafața apei. Calculați viteza de ieșire a apei.
- 3.1 Exercițiul 2
- 3.2 Exercițiul 3
- 4 Referințe
Dovada teoremei
În teorema lui Torricelli și în formula care dă viteza, se presupune că pierderile de vâscozitate sunt neglijabile, la fel ca în caz de cădere liberă, se presupune că fricțiunea datorată aerului care înconjoară obiectul care se încadrează este neglijabilă..
Presupunerea de mai sus este rezonabilă în majoritatea cazurilor și implică, de asemenea, conservarea energiei mecanice.
Pentru a demonstra teorema, vom găsi mai întâi formula pentru viteza unui obiect care este eliberat cu viteză inițială zero, de la aceeași înălțime ca suprafața lichidului din rezervor..
Principiul conservării energiei va fi aplicat pentru a obține viteza obiectului care cade chiar atunci când acesta a coborât pe o înălțime h egală cu cea de la gaură la suprafața liberă.
Deoarece nu există pierderi prin frecare, este valabil să se aplice principiul conservării energiei mecanice. Să presupunem că obiectul care cade are masa m și înălțimea h este măsurată de la nivelul de ieșire al lichidului.
Obiect care cade
Când obiectul este eliberat de la o înălțime egală cu cea a suprafeței libere a lichidului, energia sa este doar potențial gravitațional, deoarece viteza sa este zero și, prin urmare, energia sa cinetică este zero. Energia potențială Ep este dată de:
Ep = m g h
Când trece în fața găurii, înălțimea sa este zero, atunci energia potențială este zero, deci are doar energie cinetică Ec dată de:
Ec = ½ m vDouă
Deoarece energia este conservată Ep = Ec din ceea ce se obține:
½ m vDouă = m g h
Rezolvarea pentru viteză v se obține apoi formula Torricelli:
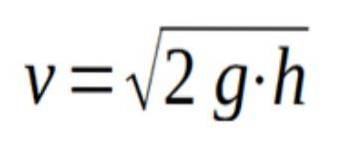
Lichid care iese din gaură
Apoi vom găsi viteza de ieșire a lichidului prin gaură, pentru a arăta că coincide cu cea care tocmai a fost calculată pentru un obiect care se încadrează liber..
Pentru aceasta ne vom baza pe principiul lui Bernoulli, care nu este altceva decât conservarea energiei aplicate fluidelor.
Principiul lui Bernoulli este formulat astfel:
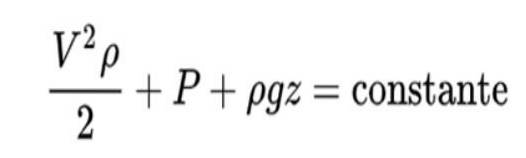
Interpretarea acestei formule este următoarea:
- Primul termen reprezintă energia cinetică a fluidului pe unitate de volum
- Al doilea reprezintă munca realizată de presiunea pe unitate de secțiune transversală.
- A treia reprezintă energia potențială gravitațională pe unitate de volum de fluid..
Deoarece pornim de la premisa că este un fluid ideal, în condiții non-turbulente cu viteze relativ mici, atunci este pertinent să afirmăm că energia mecanică pe unitate de volum în fluid este constantă în toate regiunile sau secțiunile transversale ale la fel..
În această formulă V este viteza fluidului, ρ densitatea fluidului, P presiune și z pozitie verticala.
Figura de mai jos prezintă formula Torricelli pornind de la principiul lui Bernoulli.
Aplicăm formula lui Bernoulli pe suprafața liberă a lichidului notat cu (1) și pe orificiul de ieșire notat cu (2). Nivelul zero al capului a fost ales la nivelul orificiului de ieșire.
Sub premisa că secțiunea transversală din (1) este mult mai mare decât în (2), putem presupune că rata de coborâre a lichidului din (1) este practic neglijabilă.
Acesta este motivul pentru care V1= 0, presiunea la care este supus lichidul în (1) este presiunea atmosferică și înălțimea măsurată din orificiu este h.
Pentru secțiunea de ieșire (2) presupunem că viteza de ieșire este v, presiunea la care este supus lichidul la ieșire este, de asemenea, presiunea atmosferică și înălțimea de ieșire este zero.
Valorile corespunzătoare secțiunilor (1) și (2) sunt înlocuite în formula lui Bernoulli și setate egale. Egalitatea este valabilă deoarece presupunem că fluidul este ideal și că nu există pierderi vâscoase prin frecare. Odată simplificați toți termenii, se obține viteza la orificiul de ieșire.
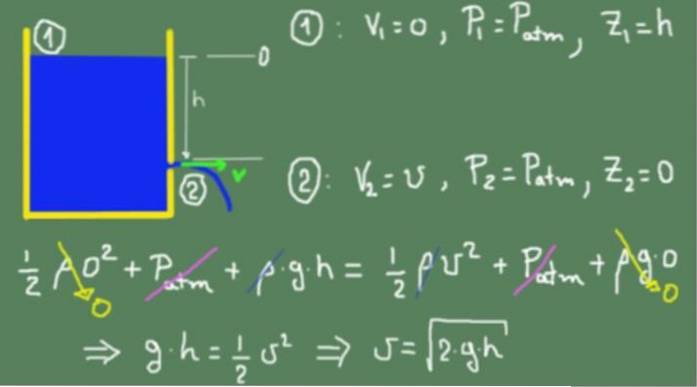
Caseta de mai sus arată că rezultatul obținut este același cu cel al unui obiect care se încadrează liber,
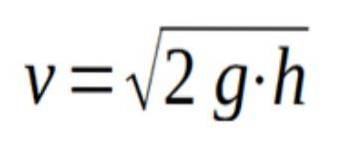
Exerciții rezolvate
Exercitiul 1
Eu) Conducta mică de evacuare a unui rezervor de apă este la 3 m sub suprafața apei. Calculați viteza de ieșire a apei.
Soluţie:
Următoarea figură arată cum se aplică formula lui Torricelli în acest caz.
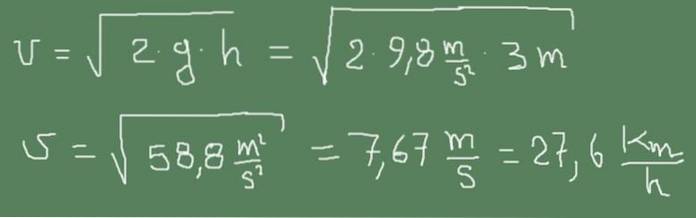
Exercițiul 2
II) Presupunând că conducta de evacuare a rezervorului din exercițiul anterior are un diametru de 1 cm, calculați debitul de evacuare a apei.
Soluţie:
Debitul este volumul de lichid care iese pe unitatea de timp și se calculează simplu prin înmulțirea zonei orificiului de ieșire cu viteza de ieșire.
Următoarea figură prezintă detaliile calculului.

Exercițiul 3
III) Determinați cât de înaltă este suprafața liberă a apei într-un recipient, dacă știți
că într-o gaură din fundul recipientului, apa iese la 10 m / s.
Soluţie:
Chiar și atunci când orificiul se află în partea de jos a containerului, formula Torricelli poate fi aplicată în continuare.
Următoarea figură arată detaliile calculelor.

Referințe
- Wikipedia. Teorema lui Torricelli.
- Hewitt, P. Științe fizice conceptuale. A cincea ediție.119.
- Tânăr, Hugh. 2016. Universitatea Sears-Zemansky Fizică cu fizică modernă. Ed. 14. Pearson. 384.



Nimeni nu a comentat acest articol încă.