Teorema lui Varignon

Care este teorema lui Varignon?

Teorema lui Varignon, în Mecanică, afirmă că suma momentelor produse de un sistem de forțe concurente față de un anumit punct este egală cu momentul forței rezultante față de același punct.

Din acest motiv, această teoremă este, de asemenea, cunoscută sub numele de începutul momentelor.

Deși primul care a enunțat-o a fost olandezul Simon Stevin (1548-1620), creatorul paradoxului hidrostatic, matematicianul francez Pierre Varignon (1654-1722) a fost cel care i-a dat ulterior forma finală.

Un exemplu al modului în care funcționează teorema lui Varignon în mecanică este următorul: să presupunem că un sistem simplu de două forțe coplanare și concurente acționează asupra unui punct F₁ Da F_Două, (notat cu aldine datorită caracterului lor vectorial). Aceste forțe dau naștere unei forțe nete sau rezultante, numită F_R.

Fiecare forță exercită un cuplu sau un moment în jurul unui punct O, care este calculat de vectorul produs între vectorul de poziție r_OP iar puterea F, Unde r_OP este direcționat de la O la punctul de concurență P:

M_O1 = r_OP × F₁

M_O2 = r_OP × F_Două

Având în vedere F_R = F₁ + F_Două, atunci:

M_SAU = r_OP × F₁ + r_OP × F_Două = M_O1 + M_O2

Dar cum r_OP este un factor comun, atunci, aplicarea proprietății distributive asupra produsului încrucișat:

M_SAU = r_OP × (F₁ + F_Două) = r_OP × F_R                

Prin urmare, suma momentelor sau cuplurilor fiecărei forțe față de punctul O este echivalentă cu momentul forței rezultante față de același punct.

Declarație și dovadă

Fie un sistem de N forțe concurente, format din F₁, F_Două, F₃... F_N, ale cărui linii de acțiune se intersectează în punctul P (vezi figura 1), momentul acestui sistem de forțe M_SAU, cu privire la un punct O este dat de:

M_SAU = r_OP × F₁ + r_OP × F_Două + r_OP × F₃ +... r_OP × F_N = r_OP × (F₁ + F_Două + F₃ +... F_N)

Demonstrație

Pentru a demonstra teorema, se utilizează proprietatea distributivă a vectorului produs între vectori.

Fii forțele F₁, F_Două, F₃... F_N aplicat punctelor A₁, LA_Două, LA₃… LA_N și simultan la punctul P. Momentul rezultat al acestui sistem, în raport cu un punct O, numit M_SAU, este suma momentelor fiecărei forțe, în raport cu punctul menționat:

M_SAU = ∑ r_OAi × F_eu

Unde suma merge de la i = 1 la i = N, deoarece există N forțe. Deoarece avem de-a face cu forțe concurente și din moment ce produsul vectorial între vectori paraleli este zero, se întâmplă că:

r_PAi × F_eu = 0

Cu vectorul nul notat ca 0.

Momentul uneia dintre forțe față de O, de exemplu cel al forței F_eu aplicat în A_eu, este scris astfel:

M_{Am auzit} = r_OAi × F_eu

Vectorul de poziție r_OAi  poate fi exprimat ca suma a doi vectori de poziție:

r_OAi = r_OP + r_PAi

În acest fel, momentul despre O al forței F_eu este:

M_{Am auzit} = (r_OP + r_PAi) × F_eu = (r_OP × F_eu) + (r_PAi × F_eu)

Dar ultimul termen este nul, după cum sa explicat mai sus, deoarece r_PAi este pe linia de acțiune a F_eu, Prin urmare:

M_{Am auzit} = r_OP × F_eu

Știind că momentul sistemului față de punctul O este suma tuturor momentelor individuale ale fiecărei forțe față de punctul respectiv, atunci:

M_SAU = ∑ M_{Am auzit} = ∑ r_OP × F_eu

Ce r_OP este constantă iese din sumă:

M_SAU = r_OP × (∑ F_eu)

Dar ∑ F_eu este pur și simplu forța netă sau forța rezultantă F_R, prin urmare, se concluzionează imediat că:

M_SAU = r_OP × F_R

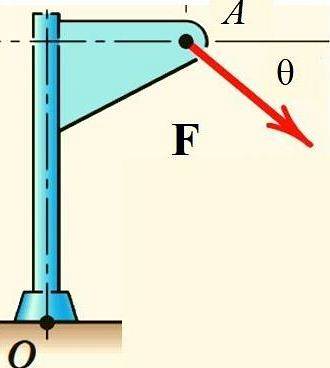
Exemplu

Teorema lui Varignon facilitează calculul momentului de forță F În ceea ce privește punctul O din structura prezentată în figură, dacă forța este descompusă în componentele sale dreptunghiulare și se calculează momentul fiecăreia dintre ele:

Aplicații ale teoremei lui Varignon

Când se cunoaște forța rezultantă a unui sistem, teorema lui Varignon poate fi aplicată pentru a înlocui suma fiecăruia dintre momentele produse de forțele care îl compun până la momentul rezultantului.

Dacă sistemul constă din forțe pe același plan și punctul cu privire la care trebuie calculat momentul aparține acelui plan, momentul rezultat este perpendicular.

De exemplu, dacă toate forțele sunt în planul xy, momentul este direcționat în axa z și rămâne doar să-i găsim magnitudinea și sensul, așa este cazul exemplului descris mai sus.

În acest caz, teorema lui Varignon ne permite să calculăm momentul rezultat al sistemului prin însumare. Este foarte util în cazul unui sistem de forță tridimensional, pentru care direcția momentului rezultat nu este cunoscută a priori.

Pentru a rezolva aceste exerciții, este convenabil să descompunem forțele și să poziționăm vectorii în componentele lor dreptunghiulare și, din suma momentelor, să determinăm componentele momentului net.

Exercițiul a fost rezolvat

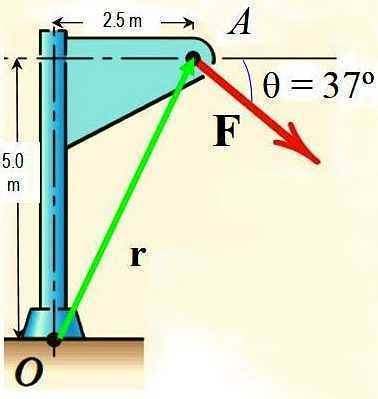
Folosind teorema lui Varignon, calculați momentul forței F în jurul punctului O prezentat în figură dacă magnitudinea lui F este de 725 N.

Soluţie

Pentru a aplica teorema lui Varignon, descompuneți forța F în două componente, ale căror momente respective în jurul lui O sunt calculate și adăugate pentru a obține momentul rezultat.

F_X = 725 N ∙ cos 37 º = 579,0 N

F_Da = - 725 N N ∙ sin 37 º = −436,3 N

În mod similar, vectorul de poziție r direcționat de la O la A are componentele:

r_X = 2,5 m

r_Da = 5,0 m

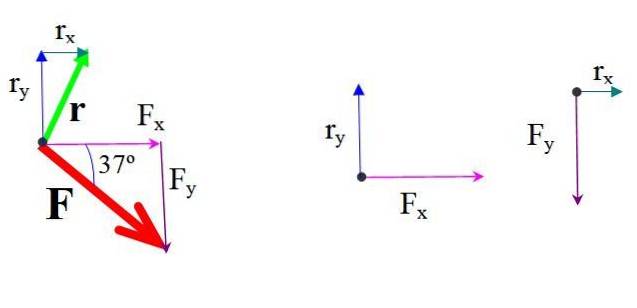
Momentul fiecărei componente a forței despre O se găsește înmulțind forța și distanța perpendiculară.

Ambele forțe tind să rotească structura în aceeași direcție, care în acest caz este în sensul acelor de ceasornic, căreia i se atribuie în mod arbitrar un semn pozitiv:

M_Bou = F_X∙ r_Da ∙ sin 90º = 579,0 N ∙ 5,0 m = 2895 N ∙ m

M_Oy = F_Da∙ r_X ∙ sin (−90º) = −436,3 N ∙ 2,5 m ∙ (−1) = 1090,8 N ∙ m

Momentul rezultat despre O este:

M_SAU = M_Bou + M_Oy = 3985,8 N ∙ m perpendicular pe plan și în sensul acelor de ceasornic.

Referințe

1. Bedford, 2000. A. Mecanica inginerească: statică. Addison Wesley. 
2. Bere, F. 2010. Static. McGraw Hill. 9. Ediție.
3. Hibbeler, R. 1992. Mecanica pentru ingineri. Al 6-lea. Ediție. CECSA.
4. HK Engineering. Teorema lui Varignon. Recuperat de pe: youtube.com.
5. Wikipedia. Teorema lui Varignon (Mecanică). Recuperat de pe: en.wikipedia.org.