Caracteristici de fotografiere parabolice, formule și ecuații, exemple

împușcare parabolică Constă în aruncarea unui obiect sau proiectil la un anumit unghi și lăsarea acestuia să se miște sub acțiunea gravitației. Dacă rezistența la aer nu este luată în considerare, obiectul, indiferent de natura sa, va urma o cale de arc parabolă.

Este o mișcare zilnică, deoarece printre cele mai populare sporturi se numără cele în care se aruncă mingi sau mingi, fie cu mâna, cu piciorul sau cu un instrument, cum ar fi o rachetă sau un liliac de exemplu.

Pentru studiul său, lovitura parabolică este împărțită în două mișcări suprapuse: una orizontală fără accelerație, iar cealaltă verticală cu accelerație constantă în jos, care este gravitația. Ambele mișcări au viteză inițială.

Să presupunem că mișcarea orizontală se desfășoară de-a lungul axei x și mișcarea verticală de-a lungul axei y. Fiecare dintre aceste mișcări este independentă de cealaltă.

Deoarece determinarea poziției proiectilului este obiectivul principal, este necesar să se aleagă un sistem de referință adecvat. Detaliile sunt mai jos.

Indice articol

• 1 Formule și ecuații de împușcare parabolică
  • 1.1 - Trajectorie, înălțime maximă, timp maxim și acoperire orizontală
• 2 Exemple de fotografiere parabolică
  • 2.1 Tragerea parabolică în activitățile umane
  • 2.2 Lovitura parabolică în natură
• 3 Exercițiu
• 4 Referințe

Formule și ecuații de împușcare parabolică

Să presupunem că obiectul este aruncat cu unghiul α în raport cu viteza orizontală și inițială v_sau așa cum se arată în figura de mai jos din stânga. Lovitura parabolică este o mișcare care are loc în avion X y și în acest caz viteza inițială se descompune astfel:

v_bou = v_sau cos α

v_Hei = v_sau sin α

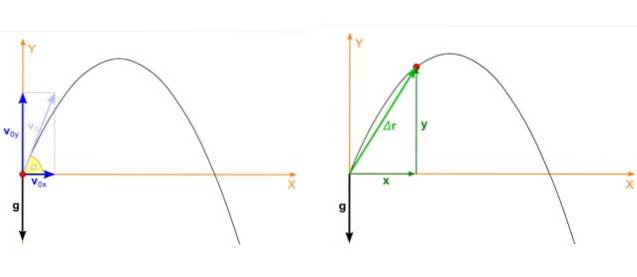
Poziția proiectilului, care este punctul roșu din figura 2, imaginea din dreapta, are, de asemenea, două componente dependente de timp, una în X iar celălalt în Da. Poziția este un vector notat ca r iar unitățile sale sunt lungime.

În figură, poziția inițială a proiectilului coincide cu originea sistemului de coordonate, deci x_sau = 0 și_sau = 0. Nu este întotdeauna cazul, puteți alege originea oriunde, dar această alegere simplifică foarte mult calculele.

În ceea ce privește cele două mișcări din x și din y, acestea sunt:

-x (t): este o mișcare rectilinie uniformă.

-y (t): corespunde unei mișcări rectilinii uniform accelerate cu g = 9,8 m / s^Două și îndreptat vertical în jos.

În formă matematică:

x (t) = v_sau cos α.t

y (t) = v_sau .sin α.t - ½g.t^Două

Vectorul de poziție este:

r (t) = [v_sau cos α.t]eu + [v_sau .sin α.t - ½g.t^Două] j

În aceste ecuații, cititorul atent va observa că semnul minus se datorează gravitației îndreptate spre sol, direcția aleasă ca fiind negativă, în timp ce în sus este luată ca pozitivă..

Deoarece viteza este prima derivată a poziției, pur și simplu derivă r (t) în ceea ce privește timpul și obține:

v (t) = v_sau cos α eu + (v_sau .sin α - gt) j

În cele din urmă, accelerația este exprimată vectorial ca:

la (t) = -g j

- Trajectorie, înălțime maximă, timp maxim și acoperire orizontală

Traiectorie

Pentru a găsi ecuația explicită a căii, care este curba y (x), trebuie să eliminăm parametrul timp, rezolvând în ecuația lui x (t) și înlocuind cu y (t). Simplificarea este oarecum laborioasă, dar în cele din urmă veți obține:

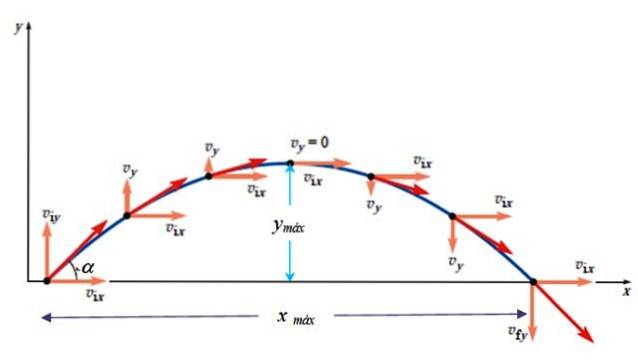
Înălțimea maximă

Înălțimea maximă apare atunci când v_Da = 0. Știind că există următoarea relație între poziție și pătratul vitezei:

v_Da^Două = v_Hei ^Două- 2gy

Face v_Da = 0 tocmai la atingerea înălțimii maxime:

0 = v_Hei ^Două- 2g. Și_max → și_max = v_Hei ^Două/ 2 g

Cu:

v_Hei = v_sau senα

Timp maxim

Timpul maxim este timpul necesar pentru a ajunge la obiect și_max. Pentru a calcula se folosește:

v_Da = v_sau .sin α - gt

Știind că v_Da devine 0 când t = t_max, rezultat:

v_sau .sin α - g.t_max = 0

t_max = v_Hei / g

Acoperire orizontală maximă și timp de zbor

Gama este foarte importantă, deoarece semnalizează unde va cădea obiectul. Astfel vom ști dacă atinge sau nu ținta. Pentru a-l găsi avem nevoie de timpul de zbor, timpul total sau t_v.

Din ilustrația de mai sus este ușor să concluzionăm că t_v = 2.t_max. Dar atenție! Acest lucru este adevărat numai dacă lansarea este nivelată, adică înălțimea punctului de plecare este aceeași cu înălțimea sosirii. În caz contrar, timpul se găsește prin rezolvarea ecuației pătratice care rezultă din înlocuirea poziției finale Da_final:

Da_final = v_sau .sin α.t_v - ½g.t_v^Două

În orice caz, acoperirea orizontală maximă este:

X_max = v_bou. t_v

Exemple de tragere parabolică

Filmarea parabolică face parte din mișcarea oamenilor și a animalelor. De asemenea, din aproape toate sporturile și jocurile în care intervine gravitația. De exemplu:

Tragerea parabolică în activitățile umane

-Piatra aruncată de o catapultă.

-Lovitura de poartă a portarului.

-Mingea aruncată de ulcior.

-Săgeata care iese din arc.

-Tot felul de salturi

-Aruncă o piatră cu o curea.

-Orice armă aruncată.

Lovitura parabolică în natură

-Apa care țâșnește din jeturi naturale sau artificiale precum cele de la o fântână.

-Pietre și lavă țâșnesc dintr-un vulcan.

-O minge care sare de pe trotuar sau o piatră care sare pe apă.

-Tot felul de animale săritoare: canguri, delfini, gazele, pisici, broaște, iepuri sau insecte, pentru a numi câteva.

Exercițiu

O lăcustă sare la un unghi de 55º cu orizontală și aterizează cu 0,80 metri înainte. Găsi:

a) Înălțimea maximă atinsă.

b) Dacă ar sări cu aceeași viteză inițială, dar formând un unghi de 45 °, ar merge mai sus??

c) Ce se poate spune despre acoperirea orizontală maximă pentru acest unghi?

Solutie la

Când datele furnizate de problemă nu conțin viteza inițială v_sau calculele sunt oarecum mai laborioase, dar din ecuațiile cunoscute se poate obține o nouă expresie. Începând de la:

X_max = v_bou . t_zbor = v_sau.cos α. t_v

Când aterizează mai târziu, înălțimea revine la 0, deci:

v_sau .sin α.t_v - ½g.t_v^Două= 0

Ce t_v este un factor comun, este simplificat:

v_sau .sin α - ½g.t_v= 0

Putem șterge t_v din prima ecuație:

t_v = x_max / v_sau.cos α

Și înlocuiți în al doilea:

v_sau .sin α - (½g.x_max / v_sau.cos α) = 0

Prin înmulțirea tuturor termenilor cu v_sau.cos αexpresia nu este modificată și numitorul dispare:

(v_sau .sin α.) (v_sau.cos α) - ½g.x_max = 0

v_sau^Două sin α. cos α = ½g.x_max

Poate fi deja șters v_sau sau, de asemenea, înlocuiți următoarea identitate:

sin 2α = 2 sin α. cos α → v_sau^Două sin 2α = g.x_max

Este calculat v_sau^Două:

v_sau^Două = g.X_max / sin 2α = (9,8 x 0,8 / sin 110) m^Două/ s^Două = 8,34 m^Două/ s^Două

Și în cele din urmă înălțimea maximă:

Da_max= v_Hei ^Două/ 2g = (8,34 x sin^Două 55) / (2 x 9,8) m = 0,286 m = 28,6 cm

Soluția b

Homarul reușește să mențină aceeași viteză orizontală, dar prin scăderea unghiului:

Da_max= v_Hei ^Două/ 2g = (8,34 x sin^Două 45) / (2 x 9,8) m = 0,213 m = 21,3 cm

Atinge o înălțime mai mică.

Soluția c

Atingerea orizontală maximă este:

X_max = v_sau^Două sen 2 / g

Prin variația unghiului, atingerea orizontală se schimbă, de asemenea:

X_max = 8,34 sen 90 / 9.8  m = 0,851 m = 85,1 cm

Saltul este mai lung acum. Cititorul poate verifica dacă este maxim pentru unghiul de 45º deoarece:

sin 2α = sin 90 = 1.

Referințe

1. Figueroa, D. 2005. Seria: Fizică pentru științe și inginerie. Volumul 1. Cinematica. Editat de Douglas Figueroa (USB).
2. Giambattista, A. 2010. Fizică. A doua editie. Dealul Mcgraw.
3. Giancoli, D. 2006. Fizică: principii cu aplicații. Al 6-lea. Ed prentice hall.
4. Resnick, R. 1999. Fizică. Vol. 1. Ediția a 3-a. În spaniolă. Compañía Editorial Continental S.A. de C.V.
5. Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 1.