
Vectori în spațiu cum să graficezi, aplicații, exerciții
A vector în spațiu este toată lumea reprezentată de un sistem de coordonate dat de X, Da Da z. Aproape întotdeauna avionul X y este planul suprafeței orizontale și a axei z reprezintă înălțimea (sau adâncimea).
Axele de coordonate carteziene prezentate în figura 1 împart spațiul în 8 regiuni numite octanți, analog cu modul în care axele X - Da împarte planul în 4 cadrane. Vom avea apoi primul octant, al doilea octant și așa mai departe.
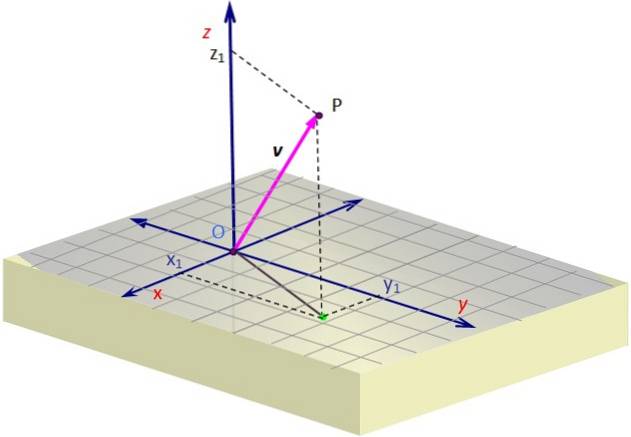
Figura 1 conține o reprezentare a unui vector v in spatiu. Este necesară o anumită perspectivă pentru a crea iluzia a trei dimensiuni pe planul ecranului, care se realizează prin desenarea unei vederi oblice.
Pentru a grafica un vector 3D, utilizați liniile punctate care determină pe grilă coordonatele proiecției sau „umbrei” v Peste suprafață X y. Această proiecție începe la O și se termină la punctul verde.
Odată ajuns acolo, trebuie să continuați de-a lungul verticalei până la înălțimea (sau adâncimea) necesară în funcție de valoarea z, până la atingerea lui P. Vectorul este desenat începând de la O și terminându-se la P, care în exemplu este în primul octant.
Indice articol
- 1 Aplicații
- 2 Notare și reprezentări de vectori în 3D
- 2.1 Unghiuri și cosinusuri directoare ale unui vector
- 3 exerciții rezolvate
- 3.1 -Exercițiunea 1
- 3.2 -Exerciția 2
- 4 Referințe
Aplicații
Vectorii din spațiu sunt folosiți pe scară largă în mecanică și alte ramuri ale fizicii și ingineriei, deoarece structurile care ne înconjoară necesită geometrie în trei dimensiuni..
Vectorii de poziționare în spațiu sunt folosiți pentru a poziționa obiecte în raport cu un punct de referință numit sursă O. Prin urmare, sunt și instrumente necesare în navigație, dar asta nu este tot.
Forțele care acționează asupra structurilor, cum ar fi șuruburile, consolele, cablurile, tijele și multe altele sunt de natură vectorială și orientate în spațiu. Pentru a-i cunoaște efectul, este necesar să îi cunoaștem adresa (și, de asemenea, punctul de aplicare).
Și frecvent direcția unei forțe este cunoscută prin cunoașterea a două puncte din spațiu care aparțin liniei sale de acțiune. În acest fel forța este:
F = F sau
Unde F este magnitudinea sau modulul forței și sau este vectorul unitar (de modul 1) îndreptat de-a lungul liniei de acțiune a F.
Notare și reprezentări vectoriale 3D
Înainte de a continua să rezolvăm câteva exemple, vom analiza pe scurt notația vectorială 3D.
În exemplul din Figura 1, vectorul v, al cărui punct de origine coincide cu originea O și al cărui capăt este punctul P, are coordonate X Da z pozitiv, în timp ce coordonata Da este negativ. Aceste coordonate sunt: X1, Da1, z1, care sunt exact coordonatele lui P.
Deci, dacă avem un vector legat de origine, adică al cărui punct de plecare coincide cu O, este foarte ușor să îi indicăm coordonatele, care vor fi cele ale punctului extrem sau P. Pentru a distinge între un punct și un vector, vom folosi până la ultimele litere aldine și paranteze, astfel:
v = < x1, Da1, z1 >
În timp ce punctul P este notat cu paranteze:
P = (x1, Da1, z1)
O altă reprezentare folosește vectori unitari eu, j Da k care definesc cele trei direcții ale spațiului pe axe X, Da Da z respectiv.
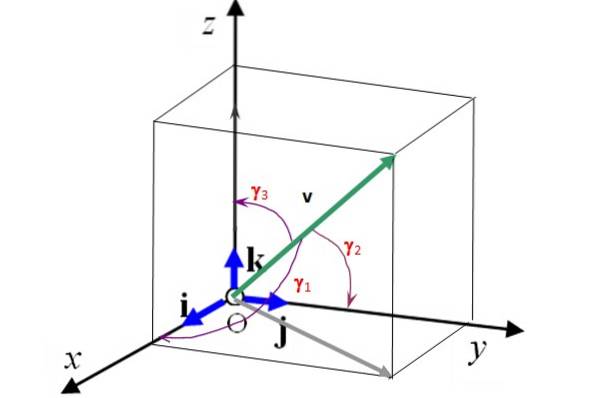
Acești vectori sunt perpendiculari între ei și formează a baza ortonormala (vezi figura 2). Aceasta înseamnă că un vector 3D poate fi scris în termenii lor ca:
v = vX eu + vDa j + vz k
Unghiuri și cosinusuri direcționare ale unui vector
Figura 2 arată, de asemenea, unghiurile de reglare γ1, γDouă și γ3 decât vectorul v face respectiv cu axele X, Da Da z. Cunoscând aceste unghiuri și mărimea vectorului, acesta este complet determinat. În plus, cosinusurile unghiurilor de director îndeplinesc următoarea relație:
(cos γ1)Două + (cos γDouă)Două + (cos γ3)Două = 1
Exerciții rezolvate
-Exercitiul 1
În figura 2 unghiurile γ1, γDouă și γ3 decât vectorul v de forma modulului 50 cu axele de coordonate sunt respectiv: 75,0º, 60,0º și 34,3º. Găsiți componentele carteziene ale acestui vector și reprezentați-l în termenii vectorilor unitari eu, j Da k.
Soluţie
Proiecție vectorială v pe axă X este VX = 50. cos 75º = 12.941. În mod similar, proiecția v pe axă Da este VDa = 50 cos 60 º = 25 și în final pe axă z este Vz = 50. cos 34.3º = 41.3. Acum v poate fi exprimat ca:
v = 12,9 eu + 25.0 j + 41.3 k
-Exercițiul 2
Găsiți tensiunile din fiecare dintre cablurile care țin cupa în figura care este în echilibru, dacă greutatea sa este de 30 N.
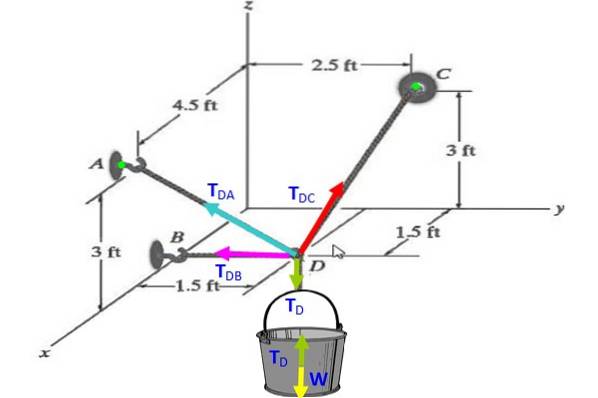
Soluţie
Pe cupă, diagrama corpului liber indică acest lucru TD (verde) compensează greutatea W (galben), deci TD = W = 30 N.
În nod, vectorul TD este direcționat vertical în jos, apoi:
TD = 30 (-k) N.
Pentru a stabili tensiunile rămase, urmați acești pași:
Pasul 1: Găsiți coordonatele tuturor punctelor
A = (4,5,0,3) (A se află pe planul peretelui x-z)
B = (1,5,0,0) (B este pe axa x)
C = (0, 2,5, 3) (C este pe planul peretelui și Z)
D = (1,5, 1,5, 0) (D este pe plan orizontal X y)
Pasul 2: Găsiți vectorii în fiecare direcție scăzând coordonatele sfârșitului și ale începutului
DĂRI = <3; -1.5; 3>
DC = <-1.5; 1; 3>
DB = <0; -1.5 ; 0>
Pasul 3: Calculați modulele și vectorii unitari
Un vector unitate se obține prin expresia: sau = r / r, cu r (cu caractere aldine) fiind vectorul și r (nu cu caractere aldine) fiind modulul vectorului menționat.
DA = (3Două + (-1,5)Două + 3Două)½ = 4,5; DC = ((-1,5) Două + 1Două + 3Două)½ = 3,5
sauDĂRI = <3; -1.5; 3>4.5 = <0.67 ; -0.33 ; 0.67>
sauDC = <-1.5; 1; 3>3,5 = <-0.43; 0.29; 0.86>
sauDB = <0; -1; 0>
sauD = <0; 0; -1>
Pasul 4: Exprimați toate tensiunile ca vectori
TDĂRI = TDĂRI sauDĂRI = TDĂRI<0.67 ; -0.33 ; 0.67>
TDC = TDC sauDC = TDC <-0.43; 0.29; 0.86>
TDB = TDB sauDB = TDB <0; -1; 0>
TD = 30 <0; 0; -1>
Pasul 5: Aplicați condiția de echilibru static și rezolvați sistemul de ecuații
În cele din urmă, condiția echilibrului static se aplică cupei, astfel încât suma vectorială a tuturor forțelor de pe nod să fie zero:
TDĂRI + TDC + TDB + TD = 0
Deoarece tensiunile sunt în spațiu, va rezulta un sistem de trei ecuații pentru fiecare componentă (X, si si z) a tensiunilor.
0,67 TDĂRI -0,43 TDC + 0 TDB = 0
-0,33 TDĂRI + 0,29 TDC - TDB = 0
0,67 TDĂRI + 0,86 TDC +0 TDB - 30 = 0
Soluția este: TDĂRI = 14,9 N; TDĂRI = 23,3 N; TDB = 1,82 N
Referințe
- Bedford, 2000. A. Mecanica inginerească: statică. Addison Wesley. 38-52.
- Figueroa, D. Seria: Fizică pentru științe și inginerie. Volumul 1. Cinematică 31-68.
- Fizic. Modulul 8: vectori. Recuperat de la: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mecanica pentru ingineri. Static. Ediția a 6-a. Compania Editura Continental. 15-53.
- Calculator de adăugare de vectori. Recuperat de la: 1728.org



Nimeni nu a comentat acest articol încă.