
Viteza areolară cum se calculează și se rezolvă exercițiile
viteza areolară este zona măturată pe unitate de timp și este constantă. Este specific fiecărei planete și apare din descrierea celei de-a doua legi a lui Kepler în formă matematică. În acest articol vom explica ce este și cum este calculat.
Boomul care reprezintă descoperirea planetelor din afara sistemului solar a reînviat interesul pentru mișcarea planetară. Nimic nu sugerează că aceste exo-planete urmează alte legi decât cele deja cunoscute și valabile în sistemul solar: legile lui Kepler..
Johannes Kepler a fost astronomul care, fără ajutorul telescopului și folosind observațiile mentorului său Tycho Brahe, a creat un model matematic care descrie mișcarea planetelor în jurul Soarelui..
A lăsat acest model întruchipat în cele trei legi care îi poartă numele și care rămân la fel de valabile astăzi ca în 1609, când a stabilit primele două și în 1618, data la care a enunțat-o pe a treia..
Indice articol
- 1 Legile lui Kepler
- 2 De ce planetele se mișcă eliptic în jurul Soarelui?
- 3 Magnitudinea vitezei liniare a unei planete nu este constantă
- 4 Viteza areolară
- 5 Calculul vitezei liniare și a vitezei areolare
- 5.1 Exercițiu
- 6 Bibliografie
Legile lui Kepler
În limbajul de astăzi, cele trei legi ale lui Kepler citesc astfel:
1. Orbitele tuturor planetelor sunt eliptice, iar Soarele este focalizat.
2. Vectorul de poziție de la Soare la o planetă mătură zone egale în timpi egali.
3. Pătratul perioadei orbitale a unei planete este proporțional cu cubul axei semi-majore a elipsei descrise..
O planetă va avea o viteză liniară, la fel ca orice obiect în mișcare cunoscut. Și există și mai multe: atunci când scriem a doua lege a lui Kepler în formă matematică, apare un nou concept numit viteza areolară, tipică fiecărei planete..
De ce planetele se mișcă eliptic în jurul Soarelui?
Pământul și celelalte planete se mișcă în jurul Soarelui datorită faptului că exercită o forță asupra lor: atracția gravitațională. La fel se întâmplă cu orice altă stea și cu planetele care alcătuiesc sistemul său, dacă le are..
Aceasta este o forță de tipul cunoscută sub numele de forță centrală. Greutatea este o forță centrală cu care toată lumea este familiarizată. Obiectul care exercită forța centrală, fie că este Soarele sau o stea îndepărtată, atrage planetele spre centrul ei și se mișcă într-o curbă închisă.
În principiu, această curbă poate fi aproximată ca o circumferință, la fel ca Nicolás Copernicus, un astronom polonez care a creat teoria heliocentrică..
Forța responsabilă este atracția gravitațională. Această forță depinde direct de masele stelei și planetei în cauză și este invers proporțională cu pătratul distanței care le separă..
Problema nu este atât de ușoară, deoarece într-un sistem solar, toate elementele interacționează în acest fel, adăugând complexitate problemei. În plus, acestea nu sunt particule, deoarece stelele și planetele au dimensiuni măsurabile..
Din acest motiv, punctul central al orbitei sau circuitului parcurs de planete nu este exact centrat pe stea, ci într-un punct cunoscut sub numele de centrul de greutate al sistemului soare-planetă..
Orbita rezultată este eliptică. Următoarea imagine o prezintă, luând ca exemplu Pământul și Soarele:
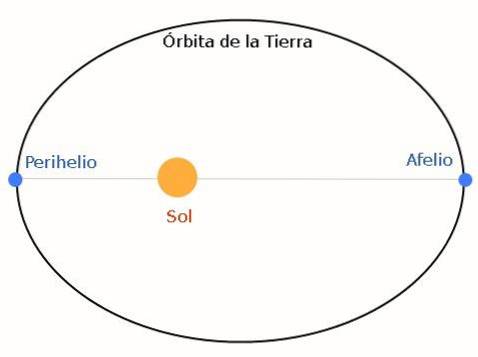
Afeliul este cea mai îndepărtată poziție de pe Soare de pe Pământ, în timp ce periheliul este punctul cel mai apropiat. Elipsa poate fi mai mult sau mai puțin turtită, în funcție de caracteristicile sistemului stea-planetă..
Valorile afeliului și periheliului variază anual, deoarece celelalte planete provoacă tulburări. Pentru alte planete, aceste poziții se numesc apoaster și respectiv periaster..
Magnitudinea vitezei liniare a unei planete nu este constantă
Kepler a descoperit că atunci când o planetă orbitează în jurul Soarelui, în timpul mișcării sale, ea măture zone egale în timpuri egale. Figura 2 arată grafic semnificația acestui lucru:
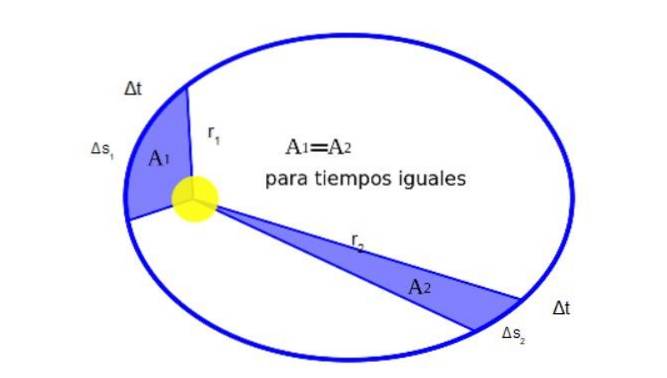
Matematic, faptul că A1 fii egal cu ADouă este exprimat astfel:

Arcurile parcurse Δs sunt mici, astfel încât fiecare zonă poate aproxima cea a unui triunghi:
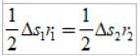
Deoarece Δs =vΔt, unde v este viteza liniară a planetei într-un punct dat, înlocuind avem:
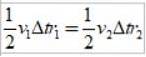
Și întrucât intervalul de timp Δt este același, obținem:
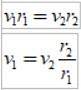
Ca rDouă > r1, apoi v1 > vDouă, cu alte cuvinte, viteza liniară a unei planete nu este constantă. De fapt, Pământul merge mai repede când este în periheliu decât atunci când este în afeliu..
Prin urmare, viteza liniară a Pământului sau a oricărei planete din jurul Soarelui nu este o magnitudine care servește la caracterizarea mișcării planetei menționate..
Viteza areolară
A doua lege a lui Kepler sugerează o nouă magnitudine numită viteza areolară. Este definită ca zona măturată pe unitate de timp și este constantă. Pentru a o calcula, se folosește următoarea figură:
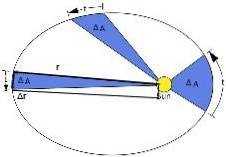
O zonă mică măturată de Pământ este aleasă în timpul realizării circuitului său eliptic, pe care îl vom denumi ca asA. Timpul necesar pentru aceasta este Δt.
Figura 3 prezintă vectorul de poziție al Pământului față de Soare, notat cu r. Când Pământul se mișcă, experimentează o deplasare Δr.
Această zonă corespunde cu jumătate din aria dreptunghiului prezentat în figura 3:
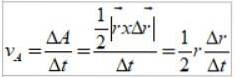
Coeficientul Δr / Δt este tocmai viteza liniară a Pământului, deci viteza areolară este următoarea:
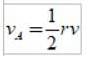
Unitățile vLA în sistemul internațional sunt:
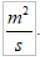
Rețineți că, deși atât r cât și v variază, produsul rămâne constant. Acest lucru face ca viteza areolară să fie o magnitudine foarte adecvată pentru a caracteriza mișcarea unei planete în jurul stelei sale..
Produsul lui r și v este magnitudinea momentului unghiular L, astfel încât viteza areolară poate fi exprimată ca:
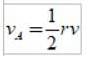
Calculul vitezei liniare și a vitezei areolare
Cu următorul exemplu vom arăta cum să calculăm viteza areolară atunci când sunt cunoscuți unii parametri ai mișcării planetare:
Exercițiu
O exo-planetă se mișcă în jurul soarelui său urmând o orbită eliptică, conform legilor lui Kepler. Când se află în periaster, vectorul său de rază este r1 = 4 107 km, iar când este în apoastro este rDouă = 15 107 km. Viteza liniară la periasterul său este v1 = 1000 km / s.
Calculati:
A) Mărimea vitezei la apoastro.
B) Viteza areolară a exo-planetei.
C) Lungimea axei semi-majore a elipsei.
Raspunde la)
Ecuația este utilizată:
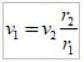
în care se substituie valorile numerice.
Fiecare termen este identificat după cum urmează:
v1 = viteza în apoastro; vDouă = viteza în periaster; r1= distanță de apoastro,
rDouă= distanța față de periaster.
Cu aceste valori obțineți:

Răspuns B)
Ecuația de utilizat este
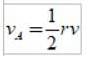
în care perechea de valori r și v a periasterului sau a apoasterului poate fi substituită, deoarece vLA este o constantă a planetei:

Răspuns C)
Lungimea axei semi-majore a elipsei este semisumul apoasterului și al periasterului:
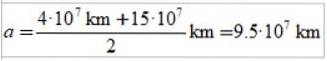
Bibliografie
- Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. Mexic. Editorii de învățare Cengage. 367-372.
- Stern, D. (2005). Trei legi ale mișcării planetare ale lui Kepler. Recuperat de la pwg.gsfc.nasa.gov
- Notă: exercițiul propus a fost preluat și modificat din următorul text dintr-o carte McGrawHill. Din păcate, este un capitol izolat în format pdf, fără titlu sau autor: mheducation.es/bcv/guide/capitulo/844817027X.pdf


Nimeni nu a comentat acest articol încă.