
Definirea vitezei instantanee, formula, calculul și exercițiile
viteza instantanee este definit ca schimbarea instantanee a deplasării în timp. Este un concept care adaugă o mare precizie studiului mișcării. Și este un avans în ceea ce privește viteza medie, ale cărei informații sunt foarte generale.
Pentru a obține viteza instantanee, să privim un interval de timp cât mai mic posibil. Calculul diferențial este instrumentul perfect pentru a exprima această idee matematic.

Punctul de plecare este viteza medie:

Această limită este cunoscută sub numele de derivat. În notația de calcul diferențial avem:
))
Ori de câte ori mișcarea este limitată la o linie dreaptă, notația vectorială poate fi eliminată.
Indice articol
- 1 Calculul vitezei instantanee: interpretare geometrică
- 2 Câteva cazuri speciale în calcularea vitezei instantanee
- 3 Exerciții rezolvate de viteză instantanee
- 3.1 Exercițiul 1
- 3.2 Exercițiul 2
- 4 Referințe
Calculul vitezei instantanee: interpretare geometrică
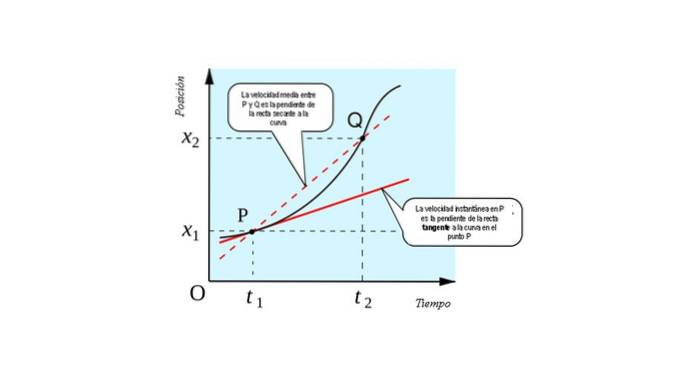
Următoarea figură arată interpretarea geometrică a conceptului derivat: este panta liniei tangentă la curbă x (t) vs. t la fiecare punct.

Vă puteți imagina cum să obțineți limita dacă punctul Q este abordat încetul cu încetul până la punctul P. Va veni un moment în care ambele puncte sunt atât de apropiate încât nu veți putea distinge una de alta..
Linia care le unește va trece apoi de la a fi secantă (linia care se intersectează în două puncte) la a fi tangentă (linia care atinge curba la un singur punct). Prin urmare, pentru a găsi viteza instantanee a unei particule în mișcare ar trebui să avem:
- Graficul poziției particulei în funcție de timp. Găsind panta liniei tangente la curbă în fiecare moment de timp, avem viteza instantanee în fiecare punct pe care îl ocupă particula.
Ei bine:
- Funcția de poziție a particulelor x (t), care este derivat pentru a obține funcția de viteză v (t), atunci această funcție este evaluată în fiecare ritm t, la comoditate. Funcția de poziție se presupune a fi diferențiată.
Câteva cazuri speciale în calcularea vitezei instantanee
-Panta liniei tangente la curba la P este 0. O pantă zero înseamnă că mobilul este staționar și că viteza sa este desigur 0.
-Panta liniei tangente la curba la P este mai mare de 0. Viteza este pozitivă. În graficul de mai sus înseamnă că mobilul se îndepărtează de O.
-Panta liniei tangente la curba la P este mai mică de 0. Viteza ar fi negativă. În graficul de mai sus nu există astfel de puncte, dar în acest caz particula s-ar apropia de O.
-Panta liniei tangente la curbă este constantă la P și la toate celelalte puncte. În acest caz, graficul este o linie dreaptă și mobilul are mișcare uniformă a liniei MRU (viteza sa este constantă).
În general, funcția v (t) este, de asemenea, o funcție a timpului, care la rândul său poate avea o derivată. Ce se întâmplă dacă nu ar fi posibil să găsim derivatele funcțiilor x (t) Da v (t)?
În cazul în care x (t) s-ar putea ca panta - viteza instantanee - să schimbe brusc semnul. Sau că ar trece imediat de la zero la o altă valoare.
Dacă da, graficul x (t) ar prezenta puncte sau colțuri în locurile schimbărilor bruște. Foarte diferit de cazul reprezentat în imaginea anterioară, în care curba x (t) este o curbă lină, fără puncte, colțuri, discontinuități sau modificări bruște.
Adevărul este că pentru telefoanele mobile reale, curbele netede sunt cele care reprezintă cel mai bine comportamentul obiectului.
Mișcarea în general este destul de complexă. Mobilele pot fi oprite pentru o vreme, accelera pentru a trece de la repaus pentru a avea o viteză și se pot îndepărta de punctul de plecare, menține viteza pentru o vreme, apoi frânează pentru a opri din nou și așa mai departe..
Din nou, ei pot începe din nou și pot continua în aceeași direcție. Sau acționați inversul și reveniți. Aceasta se numește mișcare variată într-o singură dimensiune..
Iată câteva exemple de calcul al vitezei instantanee care vor clarifica utilizarea definițiilor date:
Exerciții rezolvate de viteză instantanee
Exercitiul 1
O particulă se mișcă de-a lungul unei linii drepte cu următoarea lege a mișcării:
x (t) = -t3 + 2 tDouă + 6 t - 10
Toate unitățile sunt în sistemul internațional. Găsi:
a) Poziția particulei la t = 3 secunde.
b) Viteza medie în intervalul dintre t = 0 s și t = 3 s.
c) Viteza medie în intervalul dintre t = 0 s și t = 3 s.
d) Viteza instantanee a particulei din întrebarea anterioară, la t = 1 s.
Răspunsuri
a) Pentru a găsi poziția particulei, legea mișcării (funcția de poziție) este evaluată la t = 3:
x (3) = (-4/3) .33 + 2. 3Două + 6,3 - 10 m = -10 m
Nu există nicio problemă că poziția este negativă. Semnul (-) indică faptul că particula este la stânga originii O.
b) În calculul vitezei medii, pozițiile finale și inițiale ale particulei sunt necesare la momentele indicate: x (3) și x (0). Poziția la t = 3 este x (3) și este cunoscută din rezultatul anterior. Poziția la t = 0 secunde este x (0) = -10 m.
Deoarece poziția finală este aceeași cu poziția inițială, se concluzionează imediat că viteza medie este 0.
c) Viteza medie este raportul dintre distanța parcursă și timpul necesar. Acum, distanța este modulul sau magnitudinea deplasării, prin urmare:
distanță = | x2 - x1 | = | -10 - (-10) | m = 20 m
Rețineți că distanța parcursă este întotdeauna pozitivă.
vm = 20 m / 3 s = 6,7 m / s
d) Aici este necesar să se găsească prima derivată a poziției în raport cu timpul. Apoi este evaluat pentru t = 1 secundă.
x '(t) = -4 tDouă + 4 t + 6
x '(1) = -4,1Două + 4,1 + 6 m / s = 6 m / s
Exercițiul 2
Mai jos este graficul poziției unui mobil în funcție de timp. Găsiți viteza instantanee la t = 2 secunde.
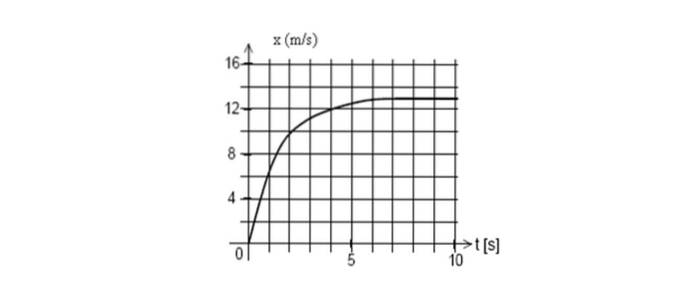
Răspuns
Desenați linia tangentă la curbă la t = 2 secunde, apoi calculați-i panta, luând oricare două puncte pe linie.
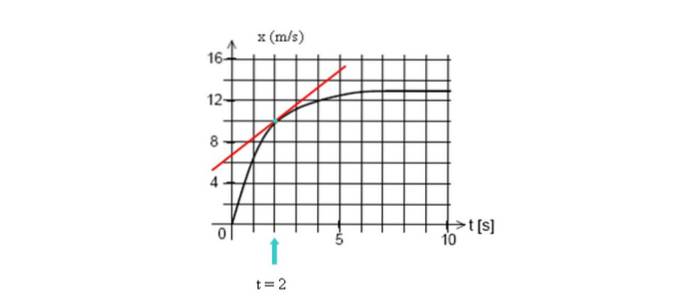
În acest exemplu vom lua două puncte care se vizualizează ușor, ale căror coordonate sunt (2 s, 10 m) și tăietura cu axa verticală (0 s, 7 m):

Referințe
- Giancoli, D. Fizică. Principii cu aplicații. 6a Ediție. Prentice Hall. 22-25.
- Resnick, R. (1999). Fizic. Volumul 1. Ediția a treia în limba spaniolă. Mexic. Compañía Editorial Continental S.A. de C.V. 21-22.
- Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. 7ma. Ediție. Mexic. Editorii de învățare Cengage. 23-25.

Nimeni nu a comentat acest articol încă.